Simulation Modeling of Truck Load of Skidding Tractors with a Grapple for Chokerless Skidding

The objective of the present study is to define mass distribution laws for a bundle of trees using the methods of statistical simulation modeling in order to calculate chokerless skidding tractors lift capacity. For that purpose a statistical simulation model has been developed to generate forest taxation data necessary for complete filling of skidding tractor grapple. The following samples have been obtained from the regions of the European North of Russia based on the model: masses of bundles of trees that can be placed in grapple and values of vertical component of normal load applied to skidding tractor grapple. Minimum values for masses of bundles may vary in the range of 40–87% from the average value. Maximum values may vary in the range of 8–55% from the average value. The difference between the maximum and minimum masses of bundle values increased with increasing the capacity grapple and decreased with increasing the distance from the butt to grapple. We have determined the dependence of bundle mass variation and values of vertical component of normal load applied to skidding tractor grapple on capacity grapple for the regions of the European North of Russia. The studies have allowed determining recommended values for chokerless skidding tractors lift capacity. The analysis of specifications of various models of skidding tractors has shown that clambunk skidders have deficient marginal lift capacity.

Simulation Modeling of Truck Load of Skidding Tractors with a Grapple for Chokerless Skidding

Ilya Shegelman, Pavel Budnik, Vyacheslav Baklagin

https://doi.org/10.5552/crojfe.2019.567

Abstract

The objective of the present study is to define mass distribution laws for a bundle of trees using the methods of statistical simulation modeling in order to calculate chokerless skidding tractors lift capacity. For that purpose a statistical simulation model has been developed to generate forest taxation data necessary for complete filling of skidding tractor grapple. The following samples have been obtained from the regions of the European North of Russia based on the model: masses of bundles of trees that can be placed in grapple and values of vertical component of normal load applied to skidding tractor grapple. Minimum values for masses of bundles may vary in the range of 40–87% from the average value. Maximum values may vary in the range of 8–55% from the average value. The difference between the maximum and minimum masses of bundle values increased with increasing the capacity grapple and decreased with increasing the distance from the butt to grapple. We have determined the dependence of bundle mass variation and values of vertical component of normal load applied to skidding tractor grapple on capacity grapple for the regions of the European North of Russia. The studies have allowed determining recommended values for chokerless skidding tractors lift capacity. The analysis of specifications of various models of skidding tractors has shown that clambunk skidders have deficient marginal lift capacity.

Keywords: bundle of trees, skidding, simulation study, statistical modeling, lift capacity

1. Introduction

Nowadays specialized tractors are used for tree skidding in timber harvesting in most countries. Chokerless tractors with arch grapple, for example Tigercat 625E, John Deere 648L, Cat 525D and clambunk skidders, for instance TimberPro Tf840, John Deere 1711d (Oprea 2008, LeDoux 2010, Ngulube et al. 2014) are widely used. Manufacturers of tractors aim to update the current models and to develop new ones. An important task at the stage of designing the main characteristics of skidding tractors is to determine the forces acting on a machine from the side of a bundle of trees. Handling the present task allows determining the skidding tractor lift capacity as well as a number of other parameters, for example the necessary compression forces of the grapple (Wang et al. 2005), engine power. Hereinafter both arch grapple and clam bunk will be referred to as grapple. Maximum allowable sheer weight of grapple will be referred to as lift capacity.

Forces acting on a machine from the side of a bundle of trees can be first determined by bundle mass of trees. Bundle mass depends on capacity grapple and characteristics of trees to be skidded. Skidding tractor grapple can contain a bundle of trees with various mass in different natural-production conditions. It is beyond the purpose of this paper to take mass of an average bundle as the initial parameter for designing specifications of skidding tractors as a considerable amount of bundle of trees will exceed this value, which will lead to increased load on a skidding tractor. Understandably, it is unpractical to take into account the bundle mass consisting of a range of large trees as the initial parameter. In practice, the chance to collect such bundles goes to zero and a skidding tractor designed for skidding such bundles would have a high price.

It can be assumed that, in order to design the main characteristics of skidding tractors, it is appropriate to take into account the mass of a bundle which, in practice, is less than or equal to the accepted value with specified probability. Such value of probability will be referred to as probability threshold. Choosing such probability threshold is a separate task requiring technical, process and economic factors to be taken into account. In our opinion, its values will be within the range of 90–99%. In order to define the bundle mass with specified probability threshold, one should be armed with mass distribution law for bundles of trees that can be formed in skidding tractor grapple in the given natural-production conditions. Therefore, the task of defining a bundle mass is rather complicated.

A lot of research is devoted to studying the efficiency of various models of chokerless skidding tractors (Kluender et al. 1997, Kluender et al. 1998, Sabo and Poršinsky 2005, Zečić 2005, Behjou et al. 2008, Spinelli and Magagnotti 2012, Vusić et al. 2013, Kulak et al. 2017). Statistic data on volumes of bundles of trees have been accumulated within such studies, and mass distribution of bundles can be obtained to a certain precision based on these data. According to Borz (2015), the number of observations in such studies ranges from 30 to 300. This number of observations is not enough to determine the distribution law applicable for the calculation of bundle mass values, according to which characteristics of skidding tractors can be determined.

A number of studies are focused on determining optimal volumes of bundles ensuring maximum output of skidding tractors based on predictive regression models (Curro and Verani 1990, Colton and Brink 1999, Ackerman at al. 2014). Such studies are based on tractor pulling forces and traction to be considered. However, the mass of a tree bundle defined in such a way is of little use for designing skidding tractors. It is conditioned by the fact that, in practice, the weight of bundles of trees is often higher than the obtained optimal value. Besides this, the optimal value is rather changeable as it depends on various natural-production conditions.

The task of defining a bundle mass can be solved based on computer statistical simulation modeling. Computer modeling in the sphere of timber harvesting has been used since the 1960s (Newnham 1968). Such studies are mostly focused on forecasting the efficiency of logging machines, expenses for timber harvesting as well as the assessment of the impact of various factors of change of efficiency and expenses for timber harvesting (McDonald et al. 2001, Wang at al. 2005, Ziesak at al. 2004, Ackerman at al. 2016, Contreras and Chung 2011, Baumgras et al. 1993, Banks et al. 1991, Ojala 1992). There is limited information about using simulation modeling to determine the mass of a tree bundle for defining forces acting on a skidding tractor from the side of a tree bundle.

The objective of the present study is to determine mass distribution laws for a bundle of trees using the methods of statistical simulation modeling in order to calculate the lift capacity of chokerless skidding tractors.

2. Material and methods

2.1 Design of the simulation experiment

In order to determine mass distribution laws for bundles of trees for chokerless skidding tractors, statistical simulation model of picking up a bundle of trees into skidding tractor grapple has been developed. The core of the simulation model is to generate taxation data of a group of trees necessary to completely fill the skidding tractor grapple. The present model has been actualized as a program (Windows application) using the syntax of С# language. The program allows getting the samples of masses of possible trees accidentally formed in grapple ( ) and values of vertical component of normal load applied to the bunk of skidding tractor ( ).

Value is to be calculated according to an expression obtained from the equation of moments of forces about point А (Fig. 1)

(1)

Where:

E[Hi] average length of trees in a bundle

Hc distance from the edge of bundle to its center of gravity

g gravitation acceleration

D distance from grapple to the center of a tree bundle

Fig. 1 Design model for

Approximate value for can be found according to the known relation .

Based on these samples, values and have been defined with the probability threshold of 90%, 95% and 99%.

Input data for the model are the following: capacity grapple ( ), distance from the butt to grapple ( ), distance from the ground to grapple when skidding ( ), diameter distribution of trees in the forest stand, height quality class of the forest stand ( ), species composition of the stand.

Trees can have different heights at the same breast height diameter. The value of establishes the relationship between breast height diameter of a tree and its height. We use to determine the height of a tree by its breast height diameter.

The simulation modeling has been performed using the example of the regions of the European North of Russia (ENR). ENR includes the following regions (Fig. 2): Murmansk Region, the Republic of Karelia, Arkhangelsk Region, Vologda Region, Komi Republic, Nenets Autonomous Area.

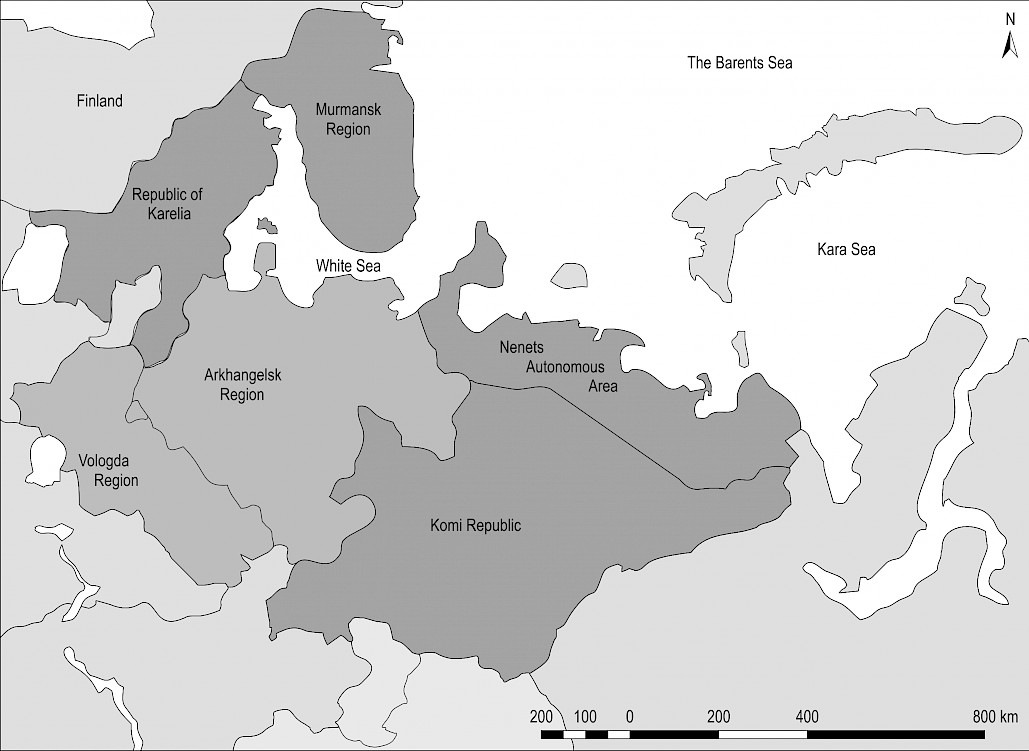
Fig. 2 Layout of ENR regions

Within the framework of a computer experiment, the algorithm of the program was repeated at least 10,000 times for given values , , and every ENR region except for Nenets Autonomous Area. The exception of Nenets Autonomous Area is related to low intensity of timber harvesting and a small amount of timber resources. The most common values for chokerless skidding tractors in the Russian Federation have been taken as given values for (m2): 1; 1.1; 1.24; 1.34; 1.48; 1.58; 1.77; 1.95; 2.2. As a matter of practice for various models, value a can be from 0.5 to 1.5 m, value – from 0.5 to 2 m (Shegelman et al. 2005). In the computer experiment, we used the following values (m): 0.5, 0.75, 1, 1.25, 1.5; and (m): 0.5, 1, 1.5, and 2.

2.2 Stages of simulation modeling

Simulation modeling includes several successive stages of generation and analysis of tree parameters. Fig. 3 shows a block diagram of the simulation model.

Fig. 3 Block diagram of the simulation model

For ENR regions, the following values of have been accepted: Murmansk Region – 3; the Republic of Karelia – 2; Arkhangelsk Region – 2; Komi Republic – 2; Vologda Region – 1. The accepted values of for the forest stands of ENR regions have been defined based on the scale of forest site quality, regional volume tables for the volumes of stem and heights, empiric distributions of diameter classes. For this purpose, average height for every height quality class has been calculated according to regional volume tables for the volumes of stem and heights using empiric distributions of diameter classes. The average heights obtained in such a way have been compared to the average heights determined as per the scale of forest site quality depending on the age of forest stand and average site quality of forest in the region. Height quality class has been selected based on the equality of values of average height obtained as per regional volume tables for the volumes of stem and heights and average height defined according to the scale of forest site quality.

The respective empiric distributions of diameter classes in a forest stand for ENR regions are used to generate value (Vinogorov 1972). Value is generated based on the information about timber resources by species (in percent for resource). Forest plans of the constituents of the Russian Federation (RF) have been the source of information. Forest plan is a state document containing a set of information about forest resources.

Value is to be defined based on digitized regional volume tables for the volumes of stem and heights used in the RF. In the simulation model, the value takes into account the reduction of the barrel length by the average stump height. The assumed average stump height is 14 cm based on the analysis of studies by Boston and Dysart (2000), Han and Renzie (2005), Repola (2008).

Set of values is calculated based on average relative stem tapers over bark by species, which are universally known data in the forest taxation of the RF. Value is to be calculated according to the formula of volume for frustum of cone for the section of stem and cone volume formula for the top. Value is to be calculated based on reference information about density of bark and the coefficient characterizing average content of bark in the volume of stem in percent. Value is calculated by multiplying together the volume of stem, excluding the volume of bark, and density of fresh wood defined as per reference information. Value is to be defined based on the studies by Barinov and Alexandrov (1988).

Value allows considering clearance area between stems in a bundle of trees and can be selected from the range of 0.5–0.6 (Shegelman et al. 2005). Value is assumed to be 0.6 in the simulation.

3. Results

As a result of the simulation experiment, 180 statistical mass distributions of bundles for each ENR region have been obtained. By way of example, Figs. 4–8 illustrate statistical mass distribution of bundles for Murmansk Region, the Republic of Karelia, Arkhangelsk Region, Komi Republic, Vologda Region obtained with the following source data: , .

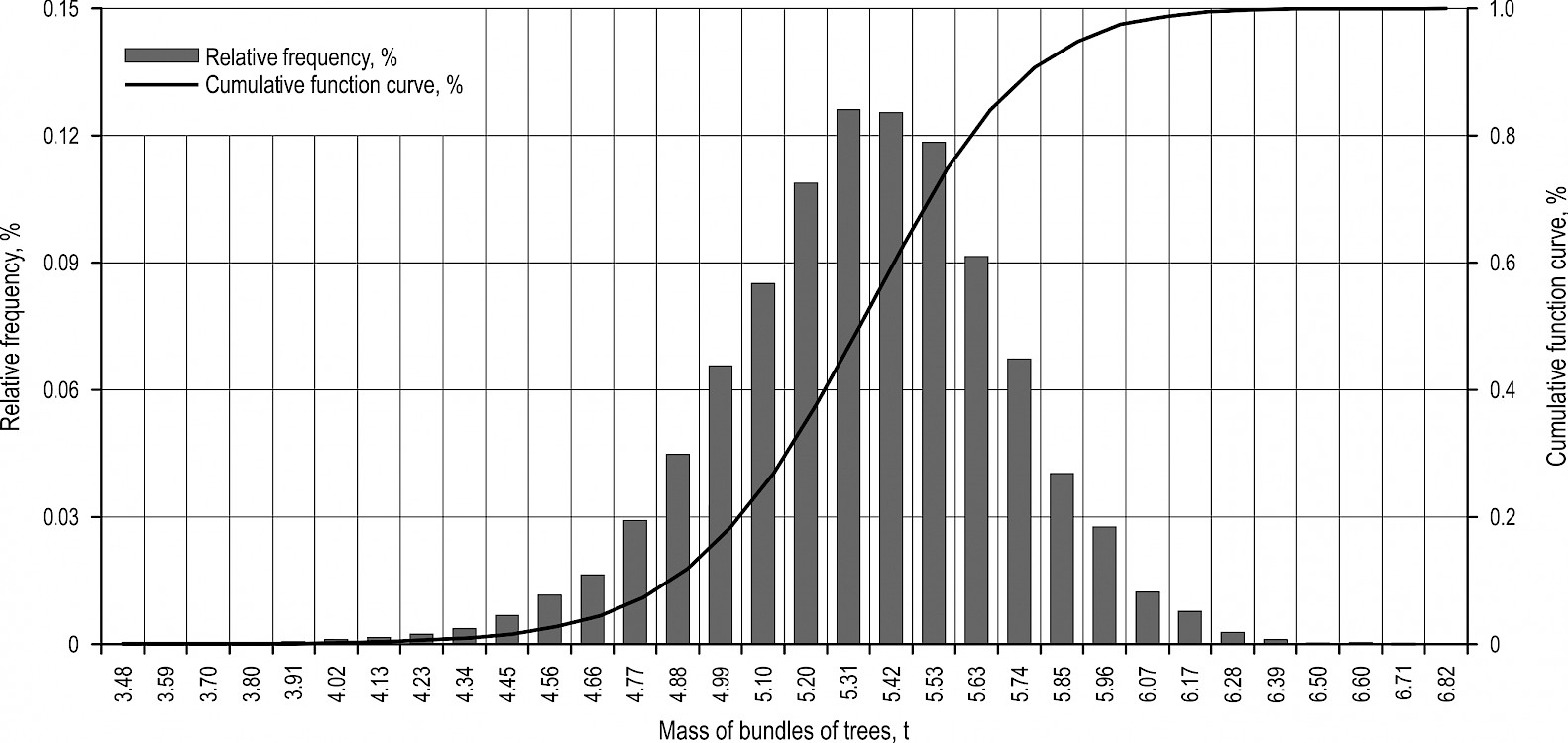
Fig. 4 Statistical mass distribution of bundles of trees for Murmansk Region

Fig. 5 Statistical mass distribution of bundles of trees for the Republic of Karelia

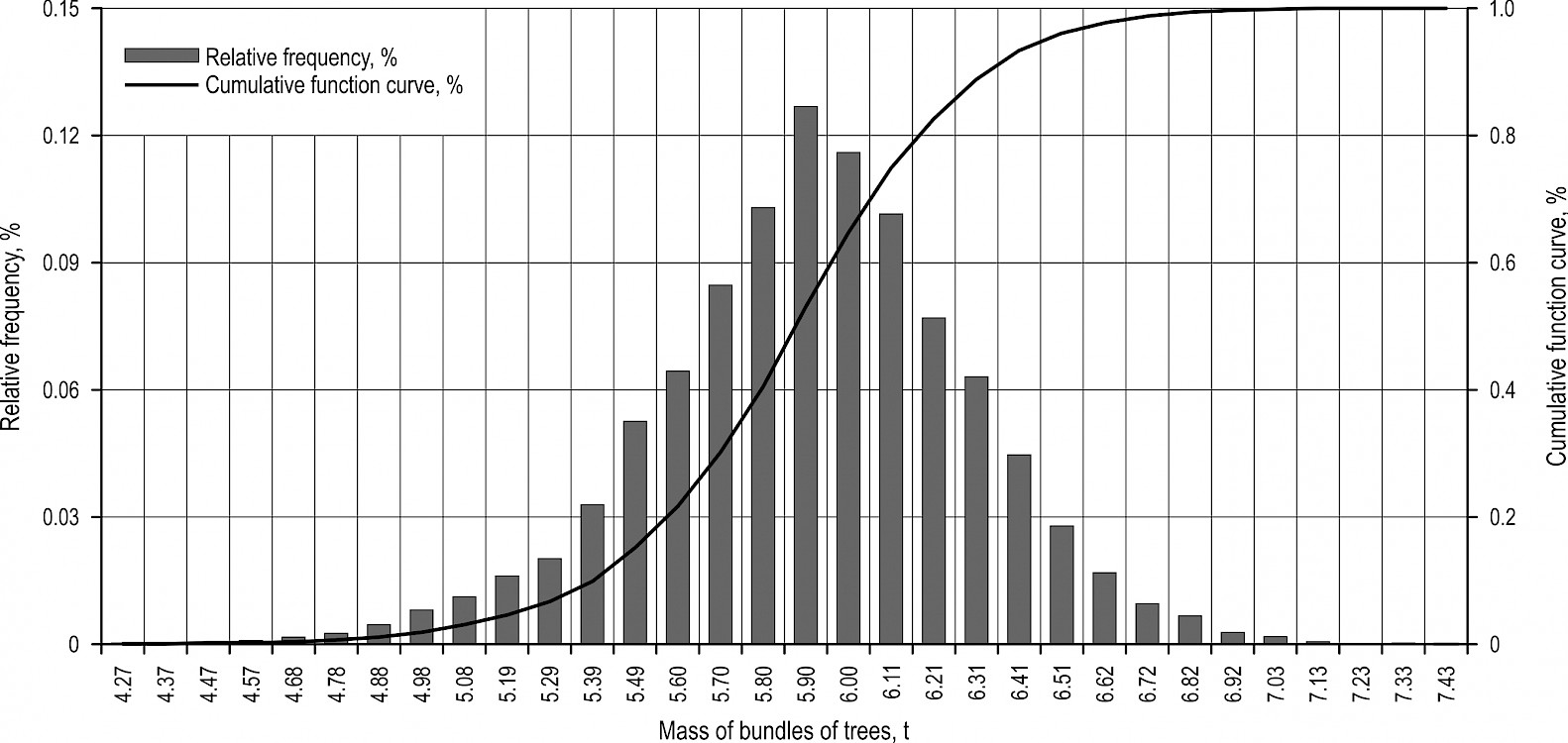
Fig. 6 Statistical mass distribution of bundles of trees for Arkhangelsk Region

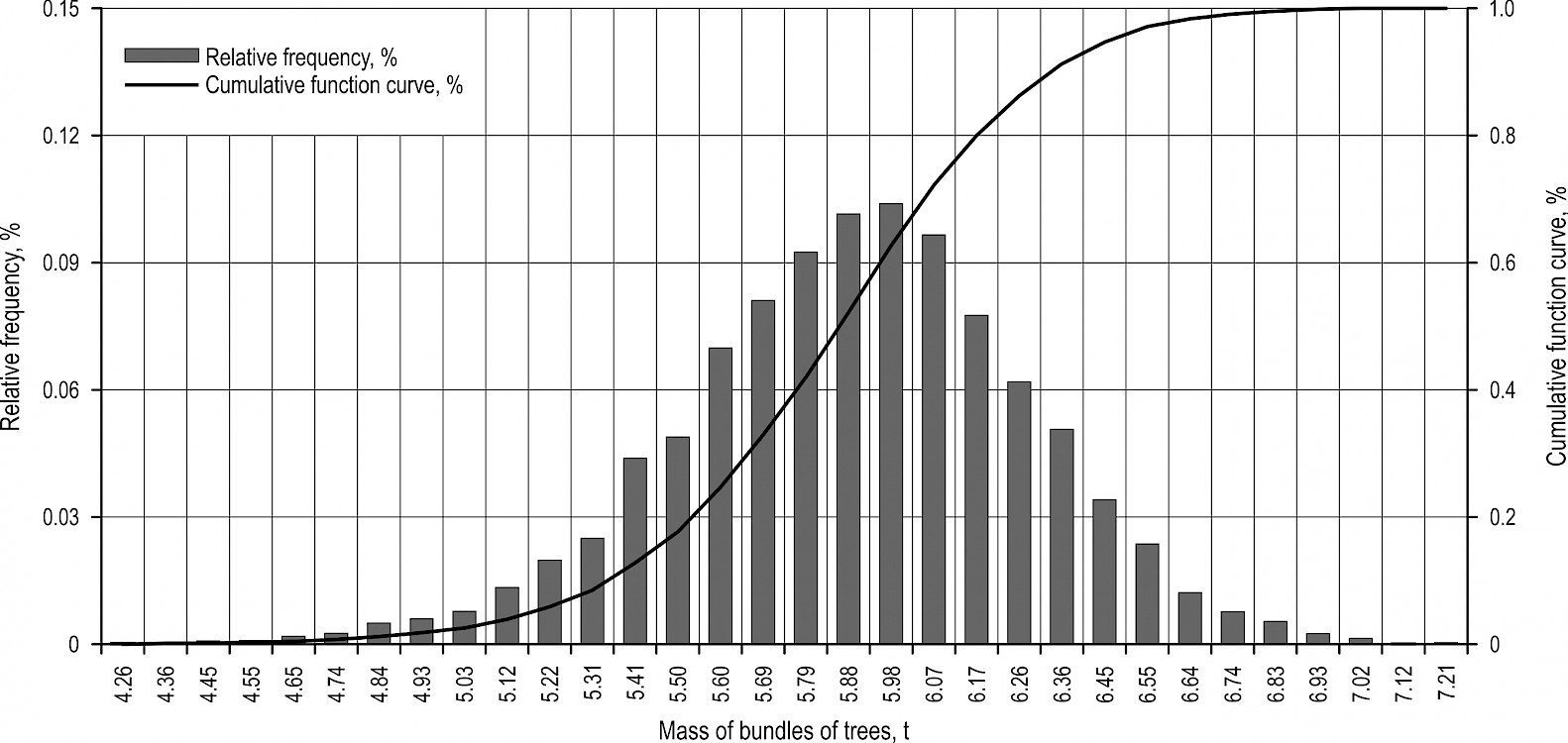
Fig. 7 Statistical mass distribution of bundles of trees for Komi Republic

Fig. 8 Statistical mass distribution of bundles of trees for Vologda Region

The analysis has shown that, with the same value , masses of a bundle of trees vary widely. Minimum values for masses of bundles have been in the range of 40–87% from the average value. Maximum values have exceeded the average value by 8–55%. The difference between the maximum and minimum masses of bundles values (range of sample) increased with increasing and decreased with increasing . The variations of masses of the tree bundle in different regions were practically negligible.

Fig. 9 illustrates average sample values for masses of bundles of trees without regional separation.

Fig. 9 Average sample values for masses of simulated tree bundles without regional separation, t

Average sample masses of bundles of trees demonstrate linear growth with the increase of values and in all the simulation experiments. Fig. 10 and 11 illustrate average sample values for masses of bundles of trees for ENR regions obtained with the following source data: and . Values of average sample masses of bundles of trees for other values are between the corresponding values shown in Fig. 10 and 11.

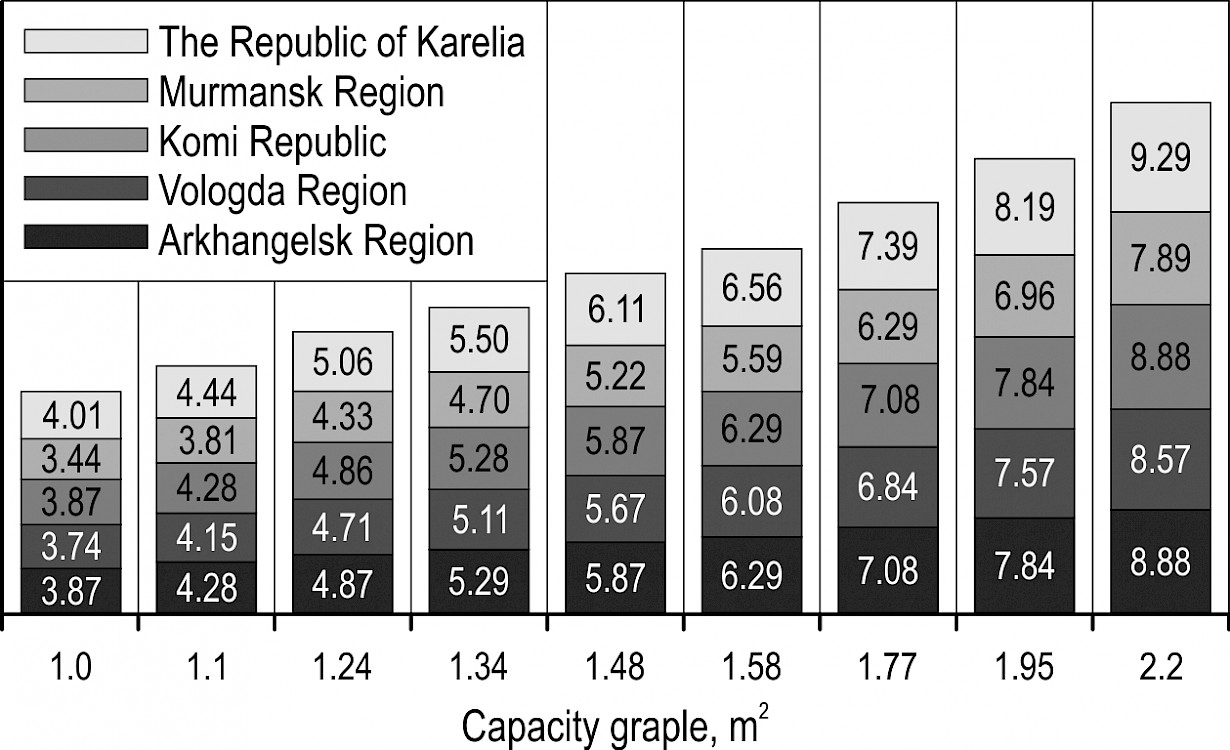
Fig. 10 Average sample values for masses of bundles of trees for ENR regions for , t

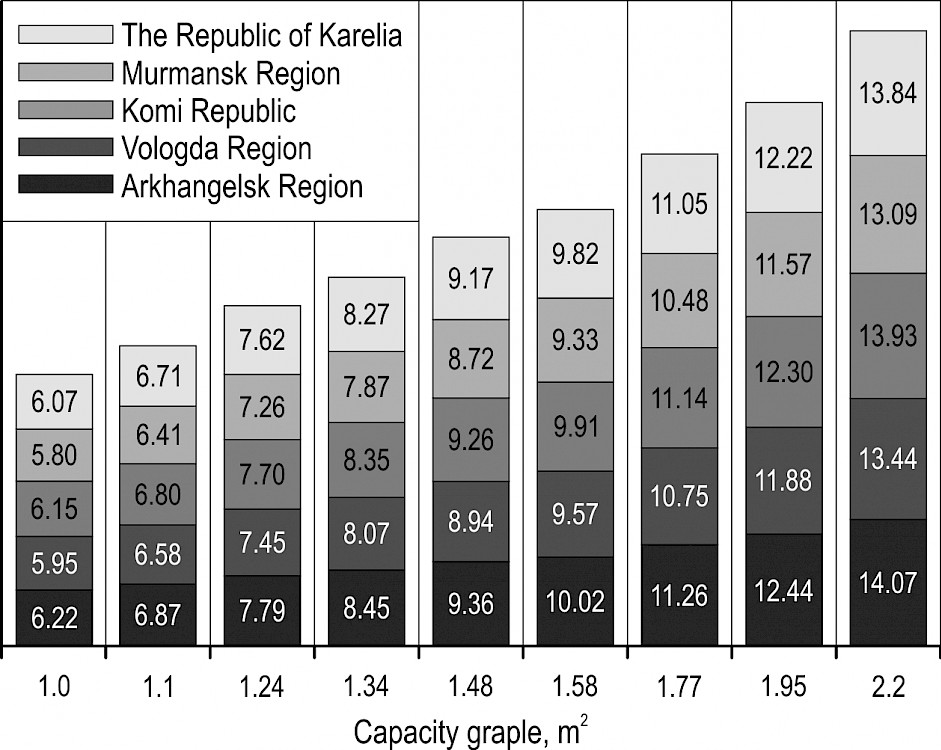
Fig. 11 Average sample values for masses of bundles of trees for ENR regions for , t

Average sample values for masses of bundles for Murmansk Region are the smallest compared to other ENR regions. The reason for this is diameter distribution and height quality class that are characteristic of lower taxation data of forest stands in Murmansk Region.

Average sample values for masses of bundles for the Republic of Karelia are the largest in all the experiments where is less than 1 m. This result is of interest due to the fact that the Republic of Karelia is described by lower forest taxation data compared to Vologda Region and forest taxation data that are close to those of Arkhangelsk Region and Komi Republic. The reason is a great variation of forest taxation data in the Republic of Karelia. In the northern part of the republic, there are forest stands with average volume of stem of 0.134 m3 (in average 0.180 m3, which is close to the index of Murmansk Region). At the same time in its southern part, average volume of stem can reach 0.351 m3 (in average 0.269 m3, which is close to the index of Vologda Region). Such variation is reflected in diameter distribution. Large diameters can be met more often (higher probability) than in other ENR regions.

Average sample values for masses of bundles for Arkhangelsk Region are the largest in all the experiments where is more than 1 m. This can be explained by the fact that increasing the value leads to an inconspicuous increase in the number of trees in a bundle. Trees with small diameters can be met more often in Arkhangelsk Region than in the Republic of Karelia. Thus, the probability that such trees can be placed in a tractor grapple is higher than that of trees with large diameters.

Forest stands of Vologda Region are featured by larger average taxation data in comparison with other ENR regions. According to the model, this is the largest height quality class. Therefore, average sample values for masses of bundles obtained for Vologda Region that have been even smaller than average sample values for Arkhangelsk Region and Komi Republic have come as a surprise. There are two reasons that can explain it. The first is the pattern of diameter distribution. First diameter classes have higher probability to appear compared to the distribution of other ENR regions. The second is the species distribution. Birch prevails in Vologda Region. Lower height against larger diameter class as compared to coniferous species (spruce and pine), which predominate in other ENR regions, is typical for this species.

Based on the computer experiment, we calculated values that will not be exceeded with 90%, 95%, 99% probability. Fig. 12–16 illustrate calculated values for , and , . Values for other and are between the corresponding values shown in Fig. 12–16. Marginal lift capacity of 25% is usually considered to be sufficient. Therefore, values shown Fig. 12–16 can be increased by 25%.

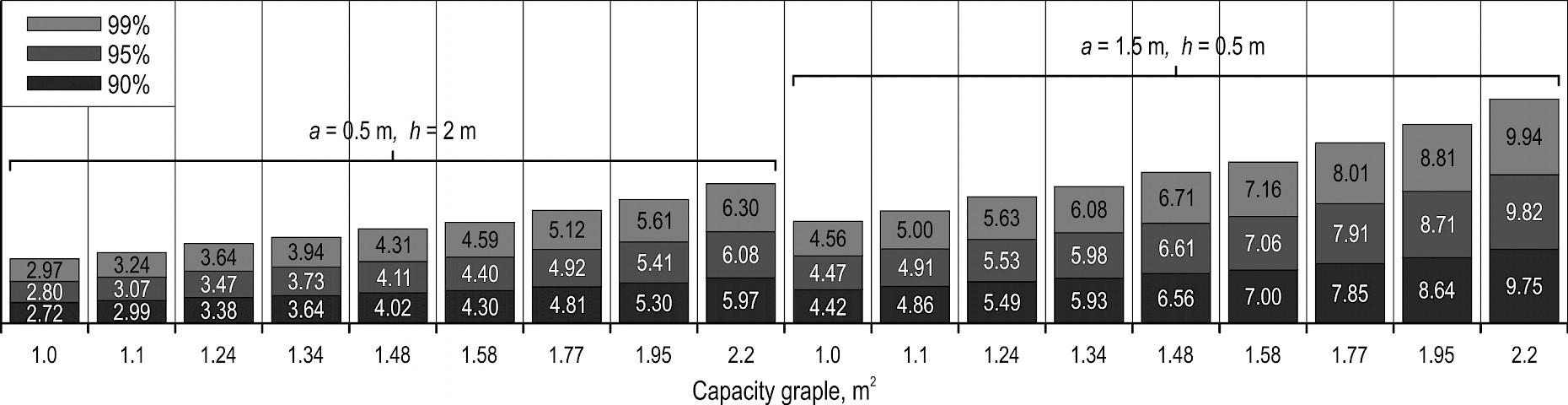
Fig. 12 Lift capacity of skidding tractor for Arkhangelsk Region, t

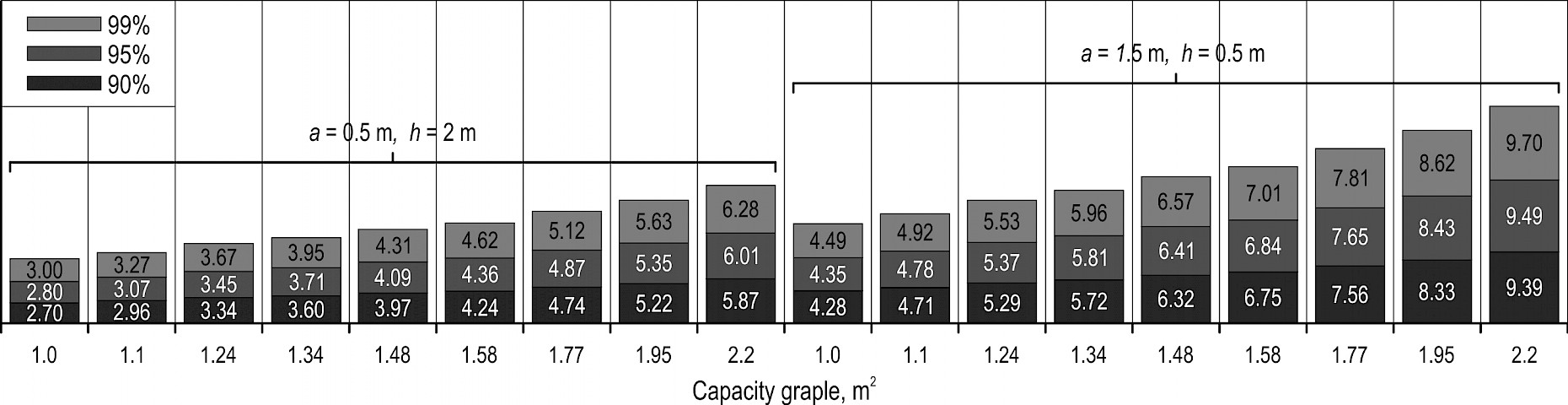
Fig. 13 Lift capacity of skidding tractor for Vologda Region, t

Fig. 14 Lift capacity of skidding tractor for Murmansk Region, t

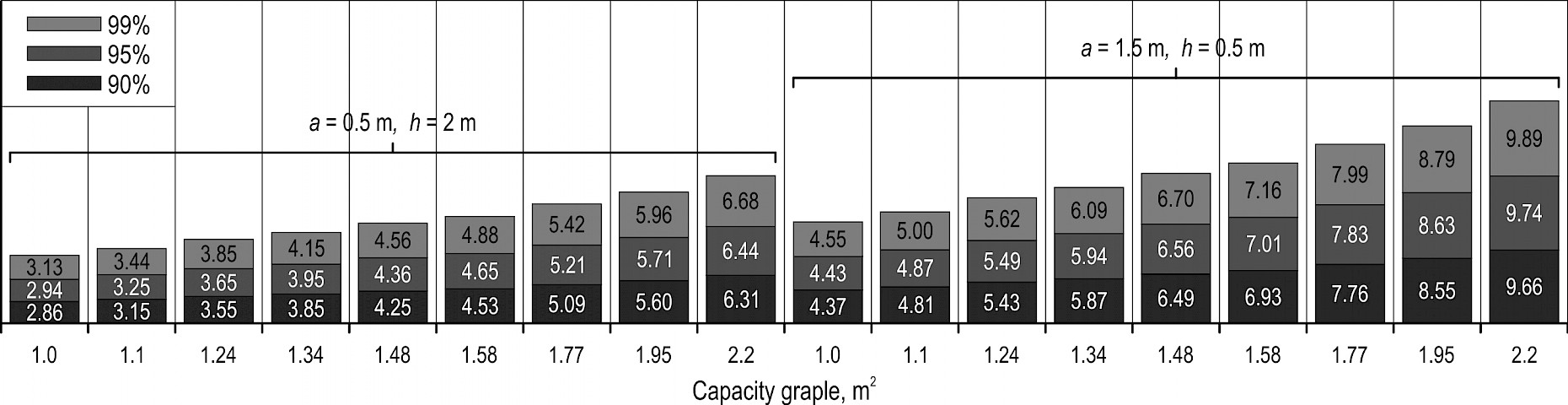
Fig. 15 Lift capacity of skidding tractor for the Republic of Karelia, t

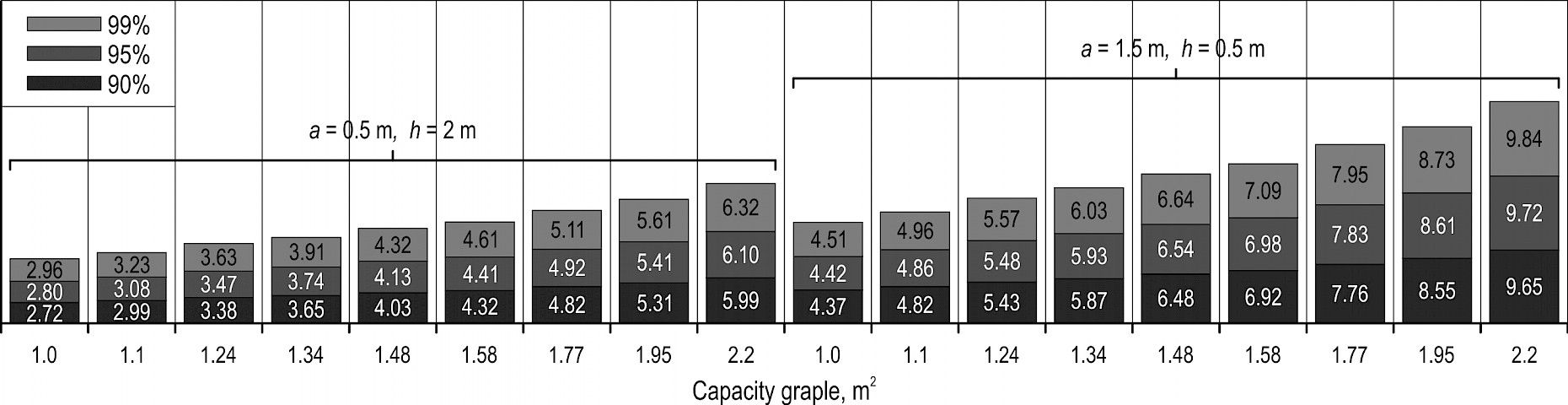
Fig. 16 Lift capacity of skidding tractor for Komi Republic, t

In order to calculate values with probability threshold of 90%, 95%, 99% and the following expression can be used:

(2)

Where:

M masses of bundles of trees with probability threshold of 90%, 95%, 99%, t, or average sample values for masses of bundles ( ), t

m1, m2, b coefficients taken according to Table 1

Table 1 Coefficients for the calculation of mass of a bundle of trees

In order to calculate values with probability threshold of 90%, 95%, 99% and the following expression can be used:

(3)

Where:

N vertical component of normal load acting on grapple with probability threshold of 90%, 95%, 99%, kN, or average sample values for vertical component of normal load applied to the bunk of skidding tractor , kN

m1, m2, m3, b coefficients taken according to Table 2

Table 2 Coefficients for the calculation of vertical component of normal load acting on grapple

The expressions [2] and [3] can be used to estimate the lift capacity of a skidding tractor with a grapple for ENR regions. For this purpose the values calculated under the expression [3] must be converted into tons. Values obtained by the expression [3] should be increased by 25% to ensure the reliability of the skidding tractor.

4. Discussion

Estimation of a mass of bundle of trees is usually carried out in studies related to the evaluation of traction characteristics of skidding tractors (Gray et al. 2016, Stoilov and Kostadinov 2009, Vechinski et al. 1998). Phillips (1983) determined the mass of a bundle of trees to calculate motive forces and fuel consumption of cable skidders. Similarly as in the present study, Phillips (1983) used the developed computer program. The forces calculation schemes underlying the computer program are similar to the calculation schemes used in our study. However, the study did not take into account the probabilistic nature of tree trunks that make up bundles. Iff et al. (1984) determined the mass of a bundle of trees to assess the performance of cable skidders. The study also used the developed computer program, which is based on the forces calculation schemes. These schemes are similar to those used in our study. The paper deals with the variation of bundles of trees. However, the distribution of trees in the forest stand was not fully taken into account. Wang and LeDoux (2003) determined the mass of a bundle of trees for assessing the performance of skidders, as well as the time needed for individual operations. Computer simulation modeling was applied in this study. Wang and LeDoux did not evaluate the lift capacity of skidders. In general, the present study deals with the development of these studies.

Based on statistical modeling for ENR regions, we have obtained statistical distribution of masses of bundles of trees that can be charged into grapple. We have defined the values of bundle masses of trees with probability thresholds of 90%, 95%, 99% and the corresponding values for vertical component of normal load acting on the skidding tractor grapple. In this way we obtained the values of lift capacity of skidding tractor with the grapple completely filled. Putting in comparison the values for lift capacity of chokerless skidding tractors obtained during our research and the values for lift capacity of certain tractors, it can be concluded that, in general, tractors have marginal lift capacity. Grapple skidders have marginal lift capacity within the range of 1–2 t, representing 20–30% of their lift capacity. Clambunk skidders (except for certain heavy-class tractors) have the margin of 3–4 t, representing 40–45% of their lift capacity. Marginal lift capacity of 25% is usually considered to be sufficient.

When using clambunk skidders, trying to increase efficiency, operators lay trees in such a way that clam bunk is not completely closed. Thus, its capacity increases, but at the same time levers of the clam bunk create the force necessary to ensure the possibility of moving a bundle of trees. As a rule, in practice such approach is applied during winter time, when soil freezes and is covered with snow, providing high bearing capacity and low resistance due to ground friction of a bundle of trees. This method can allow doubling the capacity grapple compared to the value stated in technical specifications. Such method cannot be used for grapple skidders.

According to the present analysis, when considering the possibility of skidding trees with clam bunk levers not completely closed, marginal lift capacity will be less than 1 t, about 1–10%. Such low marginal lift capacity will have an impact on the durability of machines.

Efficacy of the developed simulation model is an important issue. An extensive practical expertise in using various models of logging machines (felling-skidding machines, chokerless skidding tractors) has been accumulated in Russia. For instance chokerless skidding tractors with the capacity grapple of 1.1 m2 have been widely used in the Republic of Karelia. The results of many stop-watch studies of these tractors evidence that the average mass of a bundle of trees is within the range from 2.2 to 4.9 t. In our computer experiments, the average mass of a bundle of trees is within the range from 4.4 to 4.9 t depending on . Consequently, maximum values of bundle masses are generally within the range from 5.7 to 10 t. In our computer experiments, maximum values of bundle masses are within the range from 5.7 to 6.5 t. The variance of values obtained based on the model and the values obtained during stop-watch studies can be mostly explained by two main reasons: inaccuracies in determining the volume of a bundle during stop-watch studies (Klepac and Rummer 2000, Kluender et al. 1997); inaccuracies and simplifications of the simulation model.

Stop-watch studies record a sample of masses of bundles of trees, which is severely restricted in the number of values, which leads to a wide range of average values. Besides, the mass of a bundle of trees is calculated from the volume, which is defined approximately as it is rather complicated to determine this value under the conditions of felling area. It is necessary to consider soil conditions under which a skidding tractor is used. Soils with poor bearing capacity prevent the grapple from complete filling. Apparently, this is exactly the reason for the difference between average values of masses of bundles determined based on stop-watch studies and the values obtained in the present study.

We should also note the dependence of the modeling results on value , which can have a significant impact on the volume of a bundle. Manufacturers of skidding tractors recommend rather various values from 0.5 to 2 m, which can also be influenced by the season. In addition, in practice there is always some scatter of butts in a bundle.

Deviations from the model can also be the result of the empirical distribution of average values of breast height diameters in the regions, as well as average height quality classes used in our statistical experiments. The distribution can differ from the average distribution weighted in certain forest stands. The same situation can also apply to height quality class of a forest stand. The appropriateness of applying average-weighted distributions and average height quality classes in our analysis is open to argument. Nevertheless, when designing logging machines applicable for the whole region such data are exclusively objective factors.

Some simplification of the model expressed in taking as a constant, should also be noted. In practice changes and depends on a large variety of factors, which are difficult to consider: quality of laying trees in grapple, location in grapple and proportion of tree diameters at the level of grapple, shape of stems, etc.

The research findings can be used for handling various research tasks. Expressions [2] and [3] can be employed in design stages of logging machines in order to determine lift capacity of skidding tractors, specifications of grapple, measurement of the required engine power. Upon that, value for clambunk skidders shall be increased by multiplying by the coefficient equal to 1.1–2.2. This will allow taking into account the increase of load from a bundle of trees formed with clam bunk levers not completely closed. The obtained average sample values of bundle masses can be applied for feasibility studies, in particular, efficiency forecasting. The given values of lift capacity for various capacity grapples can be used when a logging operator chooses a certain model of machine. This is especially essential when a producer suggests installing grapples with different dimensions on a base model.

Further development of the research should focus on improving the simulation model, in particular, determining dependence of on various factors, specifying diameter distributions, models of tree stems, design models of bundle loads on grapple. Furthermore, similar research should be performed in other areas. Besides, conducting experiments for certain models of skidding tractors can become one of the directions to develop the research. Calculation of the required engine power performed on the basis of the obtained values for masses of bundles of trees can also be interesting in developing the research.

5. Conclusion

The analysis has shown that masses of bundles vary to a great extent. Minimum values for masses of bundles may vary in the range of 40–87% from the average value. Maximum values may vary in the range of 8–55% from the average value. The difference between the maximum and minimum masses of bundles values increased with increasing the capacity grapple and decreased with increasing distance from the butt to grapple. For ENR regions, the change of mass of a bundle has been related to vertical component of normal load acting on tractor grapple that will not be exceeded with probability threshold of 90%, 95%, 99% from the tractor capacity grapple. Recommended values for lift capacity of chokerless skidding tractors have been determined. The calculations have revealed that clambunk skidders have insufficient marginal lift capacity. The present work is aimed at developing knowledge in the sphere of modeling masses of bundles of trees skidded by tractors and does not claim to be comprehensive.

Acknowledgments

The research has been performed within the framework of the grant of the President of the Russian Federation № MK-5321.2018.8.

6. Reference

Ackerman, P., Pulkki, R., Gleasure, E., 2014: Modelling of wander ratios, travel speeds and productivity of cable and grapple skidders in softwood sawtimber operations in South Africa. Southern Forests: a Journal of Forest Science 76(2): 101–110. https://doi.org/10.2989/20702620.2014.917355

Ackerman, S.A., Seifert, S., Ackerman, P.A., Seifert, T., 2016: Mechanised pine thinning harvesting simulation: productivity and cost improvements as a result of changes in planting geometry. Croatian Journal of Forest Engineering 27(1): 1–15.

Banks, J., Aviles, E., McLaughlin, J., Yuan, R.C., 1991: The simulator: New member of the simulation family. Interfaces 21(2): 76–86.

Barinov, K.N., Alexandrov, V.A., 1988: Проектирование лесопромышленного оборудования (Design of forestry equipment). Publisher Leningrad University. Leningrad, 240 p.

Baumgras, J.E., Hassler, C.C., LeDoux, C.B., 1993: Estimating and validating harvesting system production through computer simulation. Forest Products Journal 43(11/12): 65–71.

Behjou, F.K, Majnounian, B., Namiranian, M., Dvořák, J., 2008: Time study and skidding capacity of wheeled skidder Timberjack 450C in Caspian forests. Journal of Forest Science 54(4): 183–188. https://doi.org/10.17221/5/2008-JFS

Borz, S.A., 2015: A review of the Romanian and international practices in skidding operation. In: XIV World forestry congress, Durban, South Africa 2015, 1–11 p.

Boston, K., Dysart, G., 2000: A comparison of felling techniques on stump height and log damage with economic interpretations. WJAА 15(2): 59–61.

Colton, A.L.C., Brink, M.P., 1999: Hitching optimal payloads increases skidder productivity. Southern African Forestry Journal 186(1): 29–32. https://doi.org/10.1080/10295925.1999.9631239

Contreras, V.A., Chung, W., 2011: A modeling approach to estimating skidding costs of individual trees for thinning operations. Western Journal of Applied Forestry 26(3): 133–146. https://doi.org/10.1093/wjaf/26.3.133

Curro, P., Verani, S., 1990: On the maximum skidding output of the »Timberjack 380« forest tractor. Journal of Forest Engineering 1(2): 35–39. https://doi.org/10.1080/08435243.1990.10702617

Gray, J.P., Vantsevich, V.V., Paldan, J., 2016: Agile tire slippage dynamics for radical enhancement of vehicle mobility. Journal of Terramechanics 65: 14–37. https://doi.org/10.1016/j.jterra.2016.01.002

Han, H.-S., Renzie, C., 2005: Effect of ground slope, stump diameter, and species on stump height for feller-buncher and chainsaw felling. International Journal of Forest Engineering 16(2): 81–88. https://doi.org/10.1080/14942119.2005.10702517

Iff, R.H., Koger, J.L., Burt, E.C., Culver, W., 1984: C-A-R-T-S: Capacity analysis of rubber-tired skidders. Transactions of the ASAE 27(3): 660–664.

Klepac, J., Rummer, R.B., 2000: Productivity and cost comparison of two different-sized skidders. Written for presentation at the 2000 ASAE Annual International Meeting, Paper No. 00-5015.

Kluender, R., Lortz, D., McCoy, W., Stokes, B., Klepac, J., 1997: Productivity of rubber-tired skidders in southern pine forests. Journal of Forest Products 47(11/12): 53–58.

Kluender, R., Lortz, D., McCoy, W., Stokes, B., Klepac, J., 1998: Removal intensity and tree size effects on harvesting cost and profitability. Forest Products Journal 48(1): 54–59.

Kluenderd, R., Lortzw, D., McCoy, W., Klepac, J., 1997: Productivity of rubber-tired skidders in southern pine forests. Forest products journal 47(11/12): 53–57.

Kulak, D., Stańczykiewicz, A., Szewczyk, S., 2017: Productivity and time consumption of timber extraction with a grapple skidder in selected pine stands. Croatian Journal of Forest Engineering 38(1): 55–63.

LeDoux, C.B., 2010: Mechanized systems for harvesting eastern hardwoods. General technical report NRS-69, Forest Service, Northern Research Station, Newtown Square, Pennsylvania, USA, 18 p.

McDonald, T.P., Rummer R.B., Taylor, S.E., 2001: Influence of bundle distance distribution and assignment sequence on tree length logging system efficiency. ASAE Ann. Int. Mtg. Pap. No. 018022.

Newnham, R.M., 1968: Simulation models in forest management and harvesting. The Forestry Chronicle 44(1): 7–13. https://doi.org/10.5558/tfc44007-1

Ngulube, E., Brink, M., Chirwa, P.W., 2014: Productivity and cost analysis of semi-mechanised and mechanised systems on the Viphya forest plantations in Malawi, Southern Forests: a Journal of Forest Science 76(4): 195–200. https://doi.org/10.2989/20702620.2014.938294

Ojala, L., 1992: Modelling approaches in port planning and analysis. Turku, Finland: Turku School of Economics and Business Administration, 1351–1381 p.

Oprea, I., 2008: Tehnologia exploatării lemnului [Timber harvesting technology]. Transilvania University Press, 273 p.

Phillips, R.A., 1983: Skidder load capacity and fuel consumption HP-4 1 C Program. U.S. government printing office. Research Paper NE-537.

Repola, J., 2008: Biomass Equations for Birch in Finland. Silva Fennica 42(4): 605–624. https://doi.org/10.14214/sf.236

Sabo, A., Poršinsky, T., 2005: Skidding of fir roundwood by Timberjack 240C from selective forests of Gorski Kotar. Croatian Journal of Forest Engineering 26(1): 13–27.

Shegelman, I.R., Skrypnik, V.I., Galaktionov, O.N., 2005: Техническое оснащение современных лесозаготовок (Technical equipment of modern logging). Profi-Inform, St.Petersburg, 344 p.

Spinelli, R., Magagnotti, N., 2012: Wood extraction with farm tractor and sulky. Estimating productivity, cost and energy consumption. Small-scale Forestry 11(1): 73–85. https://doi.org/10.1007/s11842-011-9169-8

Stoilov, S., Kostadinov, G.D., 2009: Effect of weight distribution on the slip efficiency of a four-wheel-drive skidder. Biosystems engineering 104: 486–492. https://doi.org/10.1016/j.biosystemseng.2009.08.011

Vechinski, C.R., Johnson, C.E., Raper, R.L., 1998: Evaluation of an empirical traction equation for forestry tires. Journal of Terramechanics 35(1): 55–67. https://doi.org/10.1016/S0022-4898(98)00012-3

Vinogorov, G.K., 1972: К методике обоснования расчетных деревьев при решении лесоэксплуатационных задач (To the method of substantiation of calculated trees in solving forest exploitation tasks). Works of TSNIME 122: 52–64.

Vusić, D., Šušnjar, M., Marchi, E., Spina, R., Zečić, Ž., Picchio, R., 2013: Skidding operations in thinning and shelterwood cut of mixed stands – Work productivity, energy inputs and emissions. Ecological Engineering 61: 216–223. https://doi.org/10.1016/j.ecoleng.2013.09.052

Wang, J., LeDoux, C.B., 2003: Estimating and validating ground-based timber harvesting production through computer simulation. Forest Science 49(1): 64–76. https://doi.org/10.1093/forestscience/49.1.64

Wang, J., LeDoux, C.B., Li, Y., 2005: Simulating cut-to-length harvesting operations in Appalachian hardwoods. International Journal of Forest Engineering 16(2): 11–27. https://doi.org/10.1080/14942119.2005.10702510

Wang, J., LeDoux, C.B., Wang, L., 2005: Modeling and validating the grabbing forces of hydraulic log grapples used in forest operations. International Journal of Forest Engineering 16(1): 77–85. https://doi.org/10.1080/14942119.2005.10702509

Zečić, Z., Krpan, A.P.B., Vukušić, S., 2005: Productivity of C Holder 870 F tractor with double drum winch Ingland 4002 in thinning beech stands. Croatian Journal of Forest Engineering 26(1): 49–57.

Ziesak, M., Bruchner, A-E., Hemm, M., 2004: Simulation technique for modelling the production chain in forestry. European Journal of Forest Research 123: 239–244. https://doi.org/10.1007/s10342-004-0028-4

© 2018 by the authors. Submitted for possible open access publication under the
terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Authors’ addresses:

Prof. Shegelman Ilya Romanovich, PhD

e-mail: shegelman@onego.ru

Budnik Pavel Vladimirovich, PhD *

e-mail: budnikpavel@yandex.ru

Petrozavodsk State University

Lenin str. 33

185910 Petrozavodsk

Republic of Karelia

RUSSIA

Vyacheslav Nikolayevich Baklagin, PhD

e-mail: slava.baklagin@mail.ru

Northern Water Problems Institute of the Karelian Research Centre

Russian Academy of Sciences

Aleksander Nevsky str. 50

Petrozavodsk

185910 Republic of Karelia

RUSSIA

* Corresponding author

Received: July 24, 2018

Accepted: November 27, 2018

Original scientific paper