Stem-Level Bucking Pattern Optimization in Chainsaw Bucking Based on Terrestrial Laser Scanning Data

Cross-cutting of a tree into a set of assortments (»bucking pattern«) presents a large potential for optimizing the volume and value recovery; therefore, bucking pattern optimization has been studied extensively in the past. However, it has not seen widespread adoption in chainsaw bucking, where time consuming and costly manual measurement of input parameters is required for taper curve estimation. The present study investigated an alternative approach, where taper curves are fit based on terrestrial laser scanning data (TLS), and how deviations from observed taper curves (REF) affect the result of bucking pattern optimization. In addition, performance of TLS was compared to a traditional, segmental taper curve estimation approach (APP) and an experienced chainsaw operator’s solution (CHA).

A mature Norway Spruce stand was surveyed by stationary terrestrial laser scanning. In TLS, taper curves were fit by a mixed-effects B-spline regression approach to stem diameters extracted from 3D point cloud data. A network analysis technique algorithm was used for bucking pattern optimization during harvesting. Stem diameter profiles and the chainsaw operator’s bucking pattern were obtained by manual measurement. The former was used for post-operation fit of REF taper curves by the same approach as in TLS. APP taper curves were fit based on part of the data. For 35 trees, TLS and APP taper curves were compared to REF on  tree, trunk and crown section level. REF and APP bucking patterns were optimized with the same algorithm as in TLS. For 30 trees, TLS, APP and CHA bucking patterns were compared to REF on operation and tree level.

Taper curves were estimated with high accuracy and precision (underestimated by 0.2 cm on average (SD=1.5 cm); RMSE=1.5 cm) in TLS and the fit outperformed APP. Volume and value recovery were marginally higher in TLS (0.6%; 0.9%) than in REF on operation level, while substantial differences were observed for APP (–6.1%; –4.1%). Except for cumulated nominal length, no significant differences were observed between TLS and REF on tree level, while APP result was inferior throughout. Volume and value recovery in CHA was significantly higher (2.1%; 2.4%), but mainly due to a small disadvantage of the optimization algorithm.

The investigated approach based on terrestrial laser scanning data proved to provide highly accurate and precise estimations of the taper curves. Therefore, it can be considered a further step towards increased accuracy, precision and efficiency of bucking pattern optimization in chainsaw bucking.

Stem-Level Bucking Pattern Optimization in Chainsaw Bucking Based on Terrestrial Laser Scanning Data

Gernot Erber, Christoph Gollob, Ralf Krassnitzer, Arne Nothdurft, Karl Stampfer

Abstract

Cross-cutting of a tree into a set of assortments (»bucking pattern«) presents a large potential for optimizing the volume and value recovery; therefore, bucking pattern optimization has been studied extensively in the past. However, it has not seen widespread adoption in chainsaw bucking, where time consuming and costly manual measurement of input parameters is required for taper curve estimation. The present study investigated an alternative approach, where taper curves are fit based on terrestrial laser scanning data (TLS), and how deviations from observed taper curves (REF) affect the result of bucking pattern optimization. In addition, performance of TLS was compared to a traditional, segmental taper curve estimation approach (APP) and an experienced chainsaw operator’s solution (CHA).

A mature Norway Spruce stand was surveyed by stationary terrestrial laser scanning. In TLS, taper curves were fit by a mixed-effects B-spline regression approach to stem diameters extracted from 3D point cloud data. A network analysis technique algorithm was used for bucking pattern optimization during harvesting. Stem diameter profiles and the chainsaw operator’s bucking pattern were obtained by manual measurement. The former was used for post-operation fit of REF taper curves by the same approach as in TLS. APP taper curves were fit based on part of the data. For 35 trees, TLS and APP taper curves were compared to REF on tree, trunk and crown section level. REF and APP bucking patterns were optimized with the same algorithm as in TLS. For 30 trees, TLS, APP and CHA bucking patterns were compared to REF on operation and tree level.

Taper curves were estimated with high accuracy and precision (underestimated by 0.2 cm on average (SD=1.5 cm); RMSE=1.5 cm) in TLS and the fit outperformed APP. Volume and value recovery were marginally higher in TLS (0.6%; 0.9%) than in REF on operation level, while substantial differences were observed for APP (–6.1%; –4.1%). Except for cumulated nominal length, no significant differences were observed between TLS and REF on tree level, while APP result was inferior throughout. Volume and value recovery in CHA was significantly higher (2.1%; 2.4%), but mainly due to a small disadvantage of the optimization algorithm.

The investigated approach based on terrestrial laser scanning data proved to provide highly accurate and precise estimations of the taper curves. Therefore, it can be considered a further step towards increased accuracy, precision and efficiency of bucking pattern optimization in chainsaw bucking.

Keywords: timber harvesting, motor-manual harvesting, manual bucking, optimization, point cloud, terrestrial laser scanning, taper curve

1. Introduction

In primary production environments characterized by small margins, such as forestry, efficient use of resources is crucial. During timber harvesting, trees are felled, delimbed and cross-cut (»bucked«) into a set of pieces (»bucking pattern«) of certain length, diameter, and grade (»assortments«) with a respective value. This process is a critical step in converting standing timber into end products, as it predetermines and limits the number, type and value of products that can be produced from the logs (Pnevmaticos and Mann 1972). Thus, it presents the greatest potential for optimizing volume and value recovery besides sawing of bucked logs at the mill (Faaland and Briggs 1984). Further, it greatly affects the return to the supplier and worth to the buyer in the subsequent processing and sale stages (Eng and Wythe 1982).

Bucking pattern optimization aims at »choosing the most profitable combination of log lengths, diameters and qualities, from a normally very large set of stem conversion alternatives (Näsberg 1985)« with the aim of »converting a single tree stem into smaller logs in such a way that the total stem value, according to a given price list for logs, is maximized (Näsberg 1985)«. Due to the decision complexity, mathematical modelling methods, such as linear (e.g. Smith and Harrell 1961) and dynamic programming (e.g. Pnevmaticos and Mann 1972, Faaland and Briggs 1984, Puumalainen 1998), as well as network analysis (e.g. Sessions et al. 1988), heuristic (e.g. Laroze and Greber 1997), genetic algorithm or fuzzy logic techniques (Kivinen 2007) have been considered for optimizing bucking patterns on stem, stand and forest level. In the first case, each tree pattern is optimized, while solutions are derived for stem classes or whole stands in the latter (Laroze 1999).

During the 1980s, several software programs for stem-level bucking pattern optimization were developed, e.g. AVIS in New Zealand (Geerts and Twaddle 1984) or BUCK (Oregon State University; Sessions et al. 1988). These could be operated on handheld computers and thus allowed bucking pattern optimization at the stump. Their effect on volume and value recovery was studied during several subsequent studies (Garland et al. 1989, Sessions et al. 1989, Olsen et al. 1997, Bowers 1998). In these, gross value, net value and volume recovery increases of 3.2% to 14.2%, 3.4% to 6.5% and 2.8% to 8.4% were observed, respectively.

However, differently to processing of trees by harvesters or with processors, where bucking pattern optimization is a feature offered by many manufacturers today (Labelle et al. 2017) and both individual stem value and demand restrictions are considered through value and demand matrices (Kivinen 2007), mobile device-based bucking pattern applications for use in bucking by chainsaw context have not seen substantial uptake in practice.

One of the main disadvantages in chainsaw bucking is the additional time consumption associated with the bucking pattern optimization process. For effective bucking pattern optimization, the algorithm must be fed with information about the stem form and the distribution of surface grade along its length. This information must be acquired by a visual inspection of the stem and a series of manual diameter and length measurements. From this data, the stem diameter profile along its length – the taper curve – is derived and the grades are assigned to its portions. BUCK, for example, requires measurements of stem diameter at each major change in taper, so at least at the felling cut, at the end of butt swell and topping length, as well as the measurement location. The additional time consumption for these tasks amounted to 0.8 minutes and 0.9 minutes, respectively. Thus, direct costs of felling and bucking increased by about one third due to manual measurements (Olsen et al. 1991). Even more recent applications, such as »Virtual Tree Bucking« for iOS (Corvallis Microtechnology Inc., OR, U.S.A.) or »T4E Bucking App« (Latschbacher GmbH, Kronstorf, Austria, Erber et al. 2019) for Android OS devices, require manual measurements. In case of the T4E Bucking App, they are partially estimated (felling diameter, crown base diameter, topping diameter position) from other tree parameters. However, manual measurements associated with taper curve estimation still account for about 50% of the time consumption of working with the app, not considering related data entry (Erber et al. 2021).

Terrestrial laser scanning offers the possibility to obtain taper curves efficiently and with high accuracy (Liang et al. 2014). It was employed in a bucking pattern optimization context as early as 2008 by Murphy (2008) in Douglas-fir (Pseudotsuga menziesii (Mirbel) Franco) stands. In this study, the observed total volume and stand value were found to be within 7% of actual estimates. Since then, accuracy and precision of terrestrial laser scanning and the capabilities of related applications have improved substantially. Therefore, stationary terrestrial laser scanning is currently considered the most precise system for providing 3D point cloud data in a forest environment, capable of capturing stem diameter up to 1 cm accuracy (Liang et al. 2014). These properties also make it an important component in the concept of »precision forestry«, which aims at providing and analyzing high-resolution information about forest stands to improve decision processes and forest management (Kovácsová and Antalová 2010). The range of potential applications has expanded rapidly over the last decade and includes navigation of machines in the stand (Keefe et al. 2019), forest inventory applications (Ritter et al. 2017) or support and documentation of harvesting operations (Talbot et al. 2017).

Terrestrial laser scanning constitutes a promising alternative for taper curve acquisition in chainsaw bucking, due to higher accuracy and precision of taper curve estimation and less time consumption for manual measurements during harvesting. However, neither the use of terrestrial laser scanning in bucking pattern optimization in chainsaw bucking, nor the effects of deviations between observed and estimated stem diameters on the result of bucking pattern optimization have been investigated so far.

Accordingly, the aim of the present study was to investigate if individual tree taper curves can be estimated accurately enough based on terrestrial laser scanning data by a mixed-effects B-spline regression approach to allow bucking pattern optimization in chainsaw bucking. Further, the effect of deviations between estimated and observed taper curves on the results of bucking pattern optimization was quantified. In addition, laser scanning data based taper curves were compared to taper curves derived by a segmental taper curve approach used in an earlier application. Finally, bucking patterns were compared regarding volume and value recovery between laser scanning data-based taper curves, segmental approach-based taper curves and to the pattern implemented by an experienced chainsaw operator.

2. Materials and Methods

2.1 Study Site and Operation

The study area was located near Soboth (46° 40' 21.1" N 15° 02' 10.1 "E), province of Styria, Austria, which is part of the forest enterprise Waldgut Feistritz, Staudacher & Co Holzverwertung KG. Situated between 1120 m and 1160 m a. s. l.; it has a NE aspect and is moderately sloped (25%). The site was covered by 21.5 ha, 86 year-old stand, dominated by Norway Spruce (Picea abies L.) and interspersed with single trees of European larch (Larix decidua Mill.), Fir (Abies alba Mill.) and European beech (Fagus sylvatica L.). It stocked on a highly productive (the average annual increment per hectare of 13 m³) dystric cambisoil. Natural regeneration was abundant and dominated by Norway spruce (Picea abies (L.) H. Karst.) of 0.1 to 1.0 m height. According to forest inventory, stocking volume was 649 m³ ha-1 over bark.

On a 1.2 ha harvesting area, a secondary felling treatment was performed and about one third of the total stocking volume was removed in single tree selection. Felling and processing were conducted motor-manually by two chainsaw operators employed by the forest enterprise. Trees were extracted in tree length method with a forestry tractor with winch. On the forest road, the trees were cut-to-length by a third operator and piled with the forestry tractor. Before the operation, all trees to be removed had been marked by the forest enterprise forester.

2.2 Study Layout

The study consisted of two parts, with the second drawing on the results of the first. Part one investigated the accuracy and precision of taper curve estimation based on terrestrial laser scan data and by a traditional segmental approach. It included three scenarios, each representing a different dataset and/or taper curve estimation approach. In the first (TLS), taper curves were estimated using a mixed-effects B-spline regression approach, based on terrestrial laser scanning data. Then, a segmental approach, based on manually collected tree parameters, similar to that implemented in the T4E Bucking App, was employed in the second scenario (APP). In the third scenario (REF), the taper curve was estimated by the same approach as in TLS, but based on manually collected stem diameter data. It was considered to represent the »true« taper curve, as the stem diameter could be established without the limitations of terrestrial laser scanning, namely a lack of sufficient data points in the crown layer due to shadowing effects and crown movement due to wind (Liang et al. 2014, Vaaja et al. 2016, Hyyppä et al. 2020). Therefore, it acted as reference for evaluation of taper curve estimation accuracy and precision in TLS and APP scenarios.

In part two, a modified version (preferred nominal length functionality added) of the bucking pattern optimization algorithm implemented in the T4E Bucking App was applied to each tree taper curve under the TLS, APP and REF scenarios. These were supplemented by the pattern implemented by the chainsaw operator (scenario CHA). Subsequently, TLS, APP and CHA patterns were compared to the pattern in REF to evaluate the effect of the taper curve estimation method on volume and value recovery and to compare the algorithm performance to the solution of the experienced chainsaw operator.

2.3 Field Study

2.3.1 Terrestrial Laser Scanning and Taper Curve Estimation Algorithm

In June 2020, the stand was scanned using a FARO Focus3D X330 terrestrial laser scanner (Faro Technologies Inc., Lake Mary, FL, USA). Scanning was performed in a multi-scan mode, with 28 scans in total, obtained from different positions. The scanner positions were regularly distributed across the entire area of the forest stand with a distance of 20 m between the neighboring positions. The actual scanner positions were chosen in the field, guided by visual assessment of the local visibility conditions. The coregistration of the raw scan data and the point cloud extraction were performed with FARO SCENE 6.2 software (Faro Technologies Inc., Lake Mary, FL, USA). For further details on the scanner, hardware parameter settings, scanning layout and point cloud processing, the reader is referred to Ritter et al. (2017) and Gollob et al. (2019). Because of possible shadowing effects, the 3D point clouds from stationary laser scanning can be incomplete in upper crown sections (Liang et al. 2018). To avoid that relevant data was missing, the height of each tree was additionally measured with a Vertex IV ultrasonic hypsometer (Haglöf Sweden AB, Långsele, Västernorrland, Sweden).

The stem positions and diameters were automatically derived using the methodology demonstrated in Gollob et al. (2020). The point cloud of each tree was extracted in the form of an upright-oriented cylinder centered on the tree and with a buffer width equal to diameter at breast height plus 1 m. Subsequently, these point clouds were stratified by extracting 15 cm thick slices every 50 cm along the stem length. If a layer contained less than 50 points, it was excluded from analysis. Finally, a circle, representing the stem diameter at this position was fit to each layer. To this end, the circular cluster method of Müller and Garlipp (2005), implemented in R-package »edci« (Garlipp 2018), was employed, as it is robust and efficient relative to the noise points created by branches or needles.

Finally, individual taper curves were fitted for each tree using a mixed-effects B-spline regression approach (Kublin et al. 2013), implemented in the R-package »TapeR« (Kublin and Breidenbach 2013). The data was stored in Microsoft Excel .csv files and included stem diameters estimated at 1 cm intervals.

To allow selection of the associated taper curve during bucking pattern optimization, the tree ID assigned to each tree in the point cloud was applied to all trees marked for removal by the forester with spray colour.

2.3.2 Bucking Pattern Optimization Algorithm and Settings

For bucking pattern optimization, the network analysis technique described by Sessions et al. (1988) was used. It considers stems as a network of nodes, whose spacing is defined by permissible log lengths, each with a cumulated monetary value defined by the previous logs grade, volume and price. For optimization, the path leading to the node with the largest monetary value is retraced.

The bucking pattern optimization algorithm was implemented in R statistical software (R Core Team 2018) and largely matched the T4E Bucking App prototype, described in detail in Erber et al. (2021). For the present study, it had to be modified regarding the following aspect: theoretically, industrial wood logs could have been cut to any length between 2.00 m and 4.00 m; however, the enterprise policy was to cut logs of either 2.00 m or 4.00 m length wherever possible and to consider any other lengths only if topping diameter limits could not be met. To reflect this in the algorithm, a preferred nominal length option was implemented. It prioritized the desired lengths and considered others only in case of the last log. To comply with the different taper curve estimation approaches, the prototype was adapted regarding their derivation and input. For operation, a definition of the permissible assortments in terms of nominal length, diameter class, grade and price per m³ (Table 1) was required, which was provided by the forest enterprise and entered into a Microsoft Excel sheet in the format required by the algorithm. In addition, the desired minimum topping diameter (7 cm over bark (OB)) and user-specific excess length (4 cm) were specified. The latter was added to the default excess length according to Austrian Timber Trade Guidelines (1.0% (coniferous species) or 1.5% (broadleaf species) of the nominal length, with a minimum of 6 cm, regardless of nominal length and species; Wiener Börse AG 2006).

Table 1 Permissible assortments by category, grade and respective nominal length and revenue by diameter class, provided by forest enterprise (Kremser 2020)

2.3.3 Data Collection During Harvesting

Felling and processing of trees was conducted in the period 27th–29th July, 2020 by a professional chainsaw operator with more than 30 years of experience in motor-manual harvesting operations. To avoid interference with regular work and to ensure work safety, the study trees were felled in batches of two to three in different parts of the stand. Thus, the chainsaw operator and the researchers could switch between these and maintain a safe distance. After felling and delimbing, the chainsaw operator visually assessed the surface grade along the stem and marked grades and grade borders with red spray color. In addition, he indicated his personal bucking pattern choice by scratching the bark with the chainsaw.

After the chainsaw operator had left for work in a different part of the stand, the researchers proceeded with tree data collection. Diameters were measured crosswise with a caliper in millimeter precision, and lengths were measured in centimeter precision using a forestry tape measure. Each tree species, ID, stump height (measured on the uphill side) and individual grade section lengths were established. Data was entered into a Microsoft Excel data input spreadsheet on a laptop and imported into the bucking optimization algorithm. The corresponding taper curve was selected from the filed TLS taper curves by tree ID, and trimmed to felled tree length by subtracting stump height. Subsequently, grades were allocated along the stem length as entered. The taper curve UB (under bark) was established by subtracting (double) bark thickness estimated with the function developed by Altherr et al. (1978). Based on the taper curve UB, a value-optimized bucking pattern was derived. The result was provided in tabular form of a Microsoft Excel spreadsheet. It included – for each log – tree species, nominal log length, excess length (including a cut slit allowance of 1 cm), actual log length, start, mid and end position on the stem, UB mid diameter, diameter class, grade, revenue per m³, volume UB and revenue. In addition, the estimated topping length, as well as totals of nominal log length, excess length, actual log length, volume and revenue were provided.

Each log mid-diameter position and topping length were sought out and the stem diameter was measured. If the position coincided with a knot or branch, diameters below and above were measured and averaged. If topping diameter deviated from the required limit, actual topping length was established by measuring stem diameter in upward or downward direction, until it matched. In addition, felling diameter was measured.

Finally, the bucking pattern implemented by the chainsaw operator (CHA) was established. Records included actual log length, log mid-diameter and grade.

2.4 Data Analysis

2.4.1 Preparation

In a first step, all collected data were checked for completeness, consistency, and plausibility. Analyses were carried out in R statistical software (R Core Team 2018) and Microsoft Excel.

In APP scenario, taper curves were established by the segmental approach implemented in the T4E Bucking App (Erber et al. 2021). To this end, the stem was divided into three segments, whose shape was approximated by geometric solids: Firstly, a truncated neiloid between felling diameter and DBH, secondly, a truncated cone above DBH and below crown base, and thirdly, a paraboloid above crown base in case of coniferous species. Break point diameters were derived from the pre-operation measurements (DBH), or were estimated (felling diameter and crown base diameters) by existing functions that were fitted to Austrian national forest inventory data (Eckmüllner et al. 2007). The latter functions required the elevation above sea level as input. It was set to 1.130 m, the average elevation of the harvesting site. Trunk and crown lengths were established by extracting crown base height from terrestrial laser scanning data and subtracting stump height from crown base height and crown base height and stump height from tree height.

In case of REF scenario, taper curve estimation was based on all manually measured OB stem diameters. This included the observed OB log mid-diameters in TLS and CHA bucking patterns, OB stem diameters at the estimated and actual topping length, as well as OB felling diameters. For estimation, the same method as in TLS scenario was used.

For bucking pattern optimization in APP and REF scenarios, the same algorithm as in TLS scenario was employed and results were provided in the same format.

2.4.2 Evaluation of Taper Curve Estimation Accuracy and Precision and Comparison of Bucking Patterns

Taper curves UB for each individual tree in TLS, APP and REF scenarios were merged into one dataset. Subsequently, TLS and APP taper curves were statistically compared with the REF taper curve in terms of the bias and the root mean square error (RMSE) and with respect to the felled tree stem length and the trunk and crown section level.

Five out of 35 stems had been bucked into logs and piled before the researchers were able to record the chainsaw operator’s bucking pattern. Therefore, comparison of bucking patterns had to be limited to the 30 complete datasets.

Within each scenario, every tree estimated topping length was compared to observation. If estimated topping length exceeded observation, it was checked whether the stem length at which the small end of the top end log (implemented topping length) exceeded observed topping length. If this was the case, top end logs were shortened to comply with observed topping length and their volume and value were recalculated. If the shortened log nominal length fell below the permissible minimum of 2.0 m, the log was discarded. No action was taken when observation exceeded estimated topping length, as lengthening of already cut logs was considered impractical.

TLS, APP and CHA scenario bucking patterns were compared to REF regarding the number of logs, nominal log length, volume and value recovery on operation and tree level. Deviations were described statistically and graphically. On tree level, pairwise t-tests on a 0.05 alpha-level were employed to assess statistical significance. Finally, the distribution of the assessed grades was examined in terms of the aforementioned criteria.

3. Results

3.1 Taper Curve Estimation Accuracy and Precision

In total, 35 mature Norway spruce (Picea abies (L.) H. Karst.) trees were felled, delimbed and cross-cut. Their average DBH and height were 37.2 cm (SD=6.5) and 30.94 m (SD=2.97), respectively. Mean stump height was 0.23 m (SD=0.07), while average trunk and crown lengths were 13.45 m (SD=2.93) and 17.26 (SD=3.57), respectively, which corresponded to a life crown ratio of 55.6% (SD=9.3).

OB stem diameter in TLS (–2.7% (SD=9.6)) and APP (–2.9% (SD=13.7)) was lower than in REF scenario on average (Table 2). As indicated by the substantial difference in RMSE (–0.6 cm or –28.5%), TLS taper curves provided a more accurate fit. TLS estimates of the OB stem diameter had a higher accuracy and precision, regardless of the level of measurement (whole tree, trunk and crown section level).

In the trunk section (Table 2, Fig. 1 (a) and (b)), the average deviation from REF was relatively low in both scenarios (TLS: –0.2% (SD=4.0); APP: 0.3% (SD=5.5)). Whereas the TLS estimates of the OB stem diameter showed a slight underestimation for the lower part of the trunk, the APP estimates were slightly high. For TLS, no trend regarding over- or underestimation was observed in the upper trunk. In contrast, APP showed an underestimation in this part. However, the largest deviations in both directions were observed in the root collar part below DBH; if this part was not considered, average deviations decreased considerably and RMSEs improved on tree (TLS: –0.1 cm (SD=1.3)/1.3 cm; APP: –0.8 cm (SD=1.9)/2.0 cm) and trunk level (TLS: 0.1 cm (SD=1.0)/1.0 cm; APP: 0.1 cm (SD=1.7 cm)/1.7 cm).

In the crown section, the average deviation (Table 2) of the APP estimates was considerably larger than those of TLS. APP also had a tendency to underestimate OB stem diameters at mid-crown (Fig. 1 (c) and (d)). However, this comparison also included crown section parts above the observed topping length, which are of no practical relevance to bucking pattern optimization. If these were not considered (in addition to disregarding the root collar part below DBH), average deviations decreased on tree level (TLS: –0.1 cm (SD=1.3); APP: –0.7 cm (SD=2.0)), while RMSEs did not improve (TLS: 1.3 cm; APP: 2.2 cm). On crown level, the same behavior was observed (TLS: 0.2 cm (SD=1.6)/1.6 cm; APP (–1.7 cm (SD=1.8)/2.5 cm).

Fig. 1 Deviation of over bark stem diameter from REF taper curve in TLS and APP scenario taper curves: Observation (grey) and deviation trend (LOESS fit; light gray line) for trunk and crown sections in TLS (a, c) and APP (b, d) scenarios. The black line indicates zero, the black, dashed lines 1–3 cm deviation

Table 2 Descriptive statistics of deviation of over bark stem diameter in TLS and APP scenario taper curves from REF taper curve

3.2 Bucking Pattern Comparison

3.2.1 Topping Length Estimation and Effect of Deviations

It was not possible to establish the observed topping length for two trees because of excessive stem break during felling. Thus, their estimated and observed topping length could not be compared. Investigation of the remaining 28 cases revealed that topping length underestimation occurred more frequently than exact estimation or overestimation (Table 3). Further, topping length was significantly underestimated on average in all scenarios. In case of TLS, topping diameter had been measured at the estimated topping length. Mean deviation was –1.9 cm (SD=2.4 cm), which constituted a significant underestimation (p=<0.001). Implemented topping length was shorter than the observed topping length in most cases and differences were statistically significant in all scenarios (Table 3).

In CHA scenario, implemented topping length was shorter than observed topping length in most cases and significantly shorter on average (Table 3). However, no significant deviation from REF was observed on average (p=0.753). Contrarily, average topping length was significantly shorter than in REF in TLS (p=0.021) and APP (p=0.003) scenarios.

The excess of the observed versus the implemented topping length ranged from 0.83 m (CHA) in the best case to 2.88 m (REF) in the worst case. Associated total loss of volume and value were minimal, though, and ranged from 0.01 m³ UB to 0.02 m³ UB (–0.01% to –0.03%) and 0.20 Euro to 0.55 Euro (–0.01% to –0.02%).

Table 3 Comparison of estimated topping length and implemented topping length to observed topping length. Numbers in brackets represent the respective share in the scenario total

3.2.2 Operation Level

The 30 trees bucking patterns consisted of between 205 and 214 logs (Table 4, Fig. 2a) in total. Compared to REF, a smaller number of logs was bucked in TLS (–7) and APP (–4). Cumulated nominal log length in TLS (–26.05 m; 3.3%) and APP (–73.25 m; –9.3%) was lower than with REF (Table 4, Fig. 2b). Total log volume (Table 4, Fig. 2c) in TLS was slightly larger (0.24 m³ UB; 0.6%) than in REF, while it was considerably lower (–2.60 m³ UB; –6.1%) with APP. Total value (Table 4, Fig. 2d) in TLS was 24.94 Euro (0.9%) higher than REF. Contrarily, it was distinctively lower in APP (–110.51 Euro; –4.1%).

The bucking patterns implemented by the chainsaw operator exceed that of the other scenarios in general, regardless of the parameter (Table 4, Fig. 2). However, while the number of logs (+2; 0.9%) bucked by the chainsaw operator and cumulated nominal log length were only marginally higher (0.20 m; <0.1%) than in REF, recovered volume and value recovery surpassed REF more markedly by 0.84 m³ UB (2.0%) and 64.02 Euro (2.4%).

Though grade distribution along the stem length had been the same in all scenarios, actual shares of grades differed between scenarios to some degree, and markedly between APP and the others (Table 4, Fig. 2). In APP, the share of ABC grade saw logs in total nominal log length, total volume and total value was noticeably higher. Vice versa, shares of CX saw log grade and IH industrial wood grade were lower than in all other scenarios. Comparison of APP and REF shares suggested that this can be mainly explained by considerably lower absolute values for all parameters in IH industrial wood grade, and, to a lesser degree, in saw logs grades.

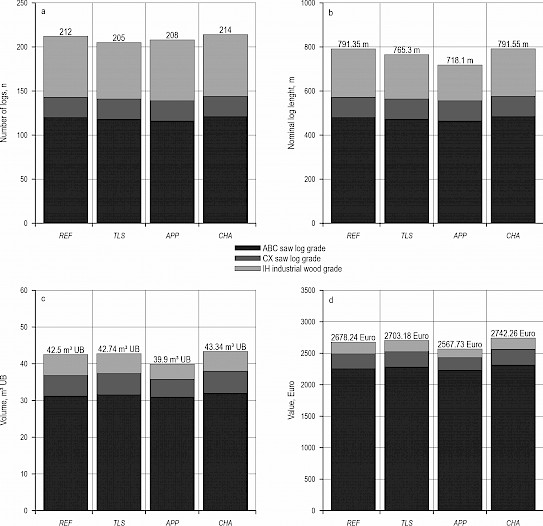
Fig. 2 Comparison of bucking patterns on operation level: totals of number of logs (a), nominal length (b), volume under bark (c) and value (d) and their distribution across grades by scenario

Table 4 Comparison of bucking pattern parameters on operation level: scenario totals and distribution across grades. Numbers in brackets represent the respective share in the scenario total

3.2.3 Tree Level

The average number of logs per tree in TLS (–3.4%) and APP (–2.0%) was slightly lower than in REF (Table 5, Table 6); contrarily, it was marginally higher in CHA (0.8%); however, none of these differences were statistically significant.

In average, the cumulated nominal length per tree (Table 5, Table 6) in TLS (–3.3%) was significantly lower than in REF, but average deviation was much smaller than in APP (–9.2%). In the latter case, average nominal log length was significantly shorter (p=<0.001) than in REF. For CHA, no significant difference in cumulated nominal length per tree was observed.

While average total volume per tree in TLS did not differ significantly from REF, the opposite was true for APP and CHA scenarios (Table 5, Table 6). In these, it was either considerably smaller (APP; –6.3%) or slightly larger (CHA; 2.1%). The pattern of significant deviations of value followed that of volume: total average value in TLS (0.9%) was slightly, but not significantly higher than in REF, while significant deviations in opposite directions were observed for APP (–4.1%) and CHA (2.4%). On a Euro per m³ basis, average value did not differ from REF in any of the scenarios.

Contrary to total tree values, on grade level, significant deviations from REF were only observed in APP scenario (Table 6). In this scenario, the average number of logs and cumulated nominal log length per tree in ABC saw log and IH industrial wood grades were lower than in REF. The same was observed for average total volume and total value per tree in case of CX saw log and IH industrial wood grades.

Table 5 Comparison of bucking pattern parameters on tree level: mean, standard deviation, min,max and median by scenario

Table 6 Deviation of TLS, APP and CHA bucking pattern parameters from TLS on tree level: mean, standard deviation and p-value by scenario and grade

4. Discussion

The applicability of terrestrial laser scanning technology has been rapidly enhanced over the last decade. However, further progress is considered as key to establish this technology in practical applications and complete digitalization of the information flow in forestry (Talbot et al. 2017). Terrestrial laser scanning has been successfully tested in forest inventory applications, in which precise stem volume estimations could be achieved through algorithms that demonstrated a high robustness under manifold scenarios (Liang et al. 2014, 2018, Gollob et al. 2019, 2020). The present study confirmed that taper curves can be estimated very accurately and precisely using laser scanning data. Further, estimation was more accurate and precise than by a traditional segmental approach. With respect to bucking pattern optimization, it entailed a more favorable result regarding volume and value recovery, which was similar to that of an experienced chainsaw operator.

The low RMSE of taper curve estimation in TLS scenario was comparable to recent studies (Liang et al. 2014, 2018, Hunčaga et al. 2020). Accuracy and precision of the estimation was higher in the (branchless) trunk section than in the crown section. This is simply because a large proportion of the laser beams is reflected by the foliage on branches in the upper tree sections (Hyyppä et al. 2020). This phenomenon results in a lack of sufficient data points in the crown layer, an issue frequently occurring in (stationary) terrestrial laser scanning (Liang et al. 2014). Further, the precision of the scan is likely affected by trees swaying in the wind (Vaaja et al. 2016). This may explain some of the observed deviations between the TLS and REF taper curves.

In some cases, the estimated taper curves did not properly fit to the manual measurements from the area near the tree top, in that the diameter observations were significantly larger than estimations. The possible explanations are manifold and include e.g. tree height measurement errors or taper irregularities caused by snow breakage. The former issue could have been resolved by extra field measurements of felled trees. However, such measurements were not conducted and would not have been possible in many cases due to frequent fragmentation of tree tops after felling. Alternatively, tree height could be derived in one pass and sufficiently accurate and precise by surveying the stand with a portable laser scanning system (PLS) (Gollob et al. 2020, Balenović et al. 2021). However, the larger deviations of the estimated stem curves might also be introduced by the natural boundary conditions of the underlying B-spline basis functions.

Taper curves could not be estimated with the same accuracy and precision by the traditional segmental approach. It should be noted, however, that this approach had originally been developed for estimation of standing tree volume in forest inventories, where it was not the aim to provide a perfect representation of the taper curve. Considering that, it performed well. However, it is particularly vulnerable to height errors by design, as tree height enters into the functions for estimating felling diameter and crown base diameter. Again, this issue could have been mitigated by measuring the crown section length in the field. However, as the decision to include the segmental approach in the comparison had been taken post-operationally, these were not conducted.

Bucking patterns established in TLS were very similar to patterns in REF, except for nominal length. This may be explained by both the slight underestimation of stem diameter in general, and a marginally larger one in the crown section, which was most likely caused by one or a combination of the abovementioned issues related to missing data points, wind and tree height.

In APP, substantially lower totals of nominal length, volume and revenue than in REF and TLS scenarios were observed across all grade categories and particularly in industrial wood grade. For higher sensitivity of APP to input parameter inaccuracies and its general tendency to underestimate upper trunk and crown section stem diameters, this was not surprising. However, deviations in volume and value were lower than in Erber et al. (2021; –8.8% and –8.6%), where broadleaf trees had been harvested.

The bucking pattern implemented by the chainsaw operator was advantageous to those of TLS and APP regarding all investigated parameters. In case of REF, differences were only marginal, and CHA advantage regarding revenue can largely be traced back to one tree. In that case, the first 3.03 m at the butt end of the stem were classified as industrial wood grade, followed by ABC saw log grade. The chainsaw operator chose to buck an industrial wood grade log of 3 m nominal length, followed by an ABC sawlog grade log. Contrarily, the bucking pattern optimization algorithm bucked a 2 m and a 4 m industrial wood grade log before continuing with ABC sawlog grade logs. This was due to the current implementation of the preferred nominal length option, which considers nominal lengths other than the preferred ones only if topping length was exceeded, but not when exceeding a grade section border. Though not comprehensible at first glance, the algorithms decision obviously rendered an optimum result under abovementioned restrictions.

Finally, it must be noted that the study was limited regarding the range of bucking alternatives, with only one permissible nominal length for the saw log assortments and two preferred permissible nominal lengths for industrial wood within a narrow range of two meters. Therefore, the bucking decision was not a very complex one, and the algorithms strengths most likely have been more apparent with more options. Due to this and to the fact that its result was compared to only one very experienced operator, no statement can be made about potential for improvement of bucking decisions by bucking pattern optimization. Answering this question would require a separate investigation, similar to Pickens et al. (1993) and ideally a controlled study in a professional training setting, with operators of different experience level.

From a time consumption and cost point of view, one may argue that stationary terrestrial laser scanning is a time-consuming endeavour and that time consumption and cost would only shift from manual measurement during harvesting to scanning of the stand and processing of the data previous to the operation. However, terrestrial laser scanning data hold considerable potential and added value for other applications, e.g. forest inventory (Gollob et al. 2019) or as a basis for the »digital twin« (Rossmann et al. 2010) of the forest in the context of digitalization and industry 4.0 applications. Therefore, it is unlikely that data would be solely collected for bucking pattern optimization and its respective share in the effort would be a minor one. Further, recent availability of mobile terrestrial laser scanning, in the form of PLS (Gollob et al. 2020, Hyyppä et al. 2020) have considerably increased survey speed, e.g. almost five times in the case of Gollob et al. (2020). Finally, data may also be collected time- and cost-efficiently by unmanned ground vehicles in the future (Pierzchała et al. 2018).

Moreover, terrestrial laser scanning is a worthwhile investment with regard to bucking pattern optimization in any case due to improved stem representation. Further, it allows to perform a rough, automated grading of the stem regarding stem geometry and surface characteristics, such as sweep, taper and branchiness before felling (Pyörälä et al. 2019), which could then be fine-tuned by the chainsaw operator on site. Finally, grading by the user could be aided by prevention of undercutting individual grade topping diameter limits, as well as pointing out mandatory cross-cutting points to avoid excessive sweep.

The bucking algorithm itself could be enhanced by more sensitive consideration of grade borders and of different types of cost to optimize contribution margins. To better match contractual obligations, demand restrictions could be implemented, similar to harvesters (Kivinen et al. 2007).

Successful implementation of bucking pattern optimization in chainsaw bucking, however, will largely depend on whether it can be integrated into an easy-to-use system. As the present study showed, terrestrial laser scanning clearly enhances the process by replacing a significant proportion of manual measurements related to taper curve estimation. By operating the algorithm on a device with a larger screen (e.g. a small, rugged tablet), usability could be facilitated further. However, having to take off gloves for data entry may add discomfort, especially in wintertime. To avoid manual entry, a mixed-reality solution integrated into the chainsaw operator’s helmet, as demonstrated by Wagner (2019), supplemented by voice control could be employed.

5. Conclusions

The proposed approach for acquiring stem diameter data and fitting of taper curves for bucking pattern optimization provided estimations of taper curves with high precision and accuracy, on tree, trunk and crown section level, and was favorable to that of a traditional segmental approach in all aspects. Therefore, the investigated approach can be considered very well suited for the task. However, its application suffered from the typical challenges of terrestrial laser scanning, and that of stationary types in particular (shadowing effects, wind). Therefore, and to further reduce the time consumption for data aqusition, future developments should focus on portable terrestrial laser scanning platforms and on integrating procedures to aid the grading process (stem geometry, surface characteristics).

The adequacy of the approach was also reflected by the result of the bucking pattern optimization, which was superior to that of the traditional approach and comparable to an experienced chainsaw operator’s solution. The latter’s slight advantage regarding value recovery resulted from an issue in the bucking pattern optimization algorithm, which can be easily resolved by reprogramming. Considering the chainsaw operator’s inherent advantage regarding awareness of tree dimensions, the investigated approach performed highly satisfactorily.

For its enhancement of the optimization result and substantial reduction of time consumption for manual measurements, the investigated approach can be considered a further step towards increased accuracy, precision and efficiency of bucking pattern optimization in chainsaw bucking.

Acknowledgments

The research leading to these results was conducted as part of Digi4+ project. This project has received funding from Austrian Federal Ministry of Agriculture, Regions and Tourism under grant agreement No 101470.

The Authors also thank Mr. Franz Gollob and Mr. Philipp Waltl for their valuable assistance with data collection. Special thanks to forest enterprise Waldgut Feistritz, Staudacher & Co Holzverwertung KG, represented by Patrick Kremser, for allowing access to their operation and offering full support to the experiment.

6. References

Altherr, E., Unfried, P., Hradetzky, J., Hradetzky, V., 1978: Statistische Rindenbeziehungen als Hilfsmittel zur Ausformung und Aufmessung unentrindeten Stammholzes: Teil IV: Fichte, Tanne, Douglasie und Sitka-Fichte; Forstliche Versuchs- und Forschungsanstalt Baden-Württemberg, Germany, 294 p.

Balenović, I., Liang, X., Jurjević, L., Hyyppä, J., Seletković, A., Kukko, A., 2021: Hand-held personal laser scanning – Current status and perspectives for forest inventory application. Cro. J. For. Eng. 42(1): 165–183. https://doi.org/10.5552/crojfe.2021.858

Bowers, S., 1998: Increased value through optimal bucking. West. J. Appl. For. 13(3): 85–89. https://doi.org/10.1093/wjaf/13.3.85

Eckmüllner, O., Schedl, P., Sterba, H., 2007: Neue Schaftkurven für die Hauptbaumarten Österreichs und deren Ausformung in marktkonforme Sortimente. Austrian J. For. Sci. 124(3–4): 215–236.

Eng, G., Whyte, A.G.D., 1982: Optimal tree bucking. Proceedings of 18th annual ORSNZ conference Canterbury, New Zealand, 23–24th August. Operational Research Society of New Zealand: Auckland, New Zealand, 91–98.

Erber, G., Viertbauer, M., Schildberger, V., 2019: T4E Bucking App – A mobile device based application for value-optimized motor-manual bucking – manual, version 1.3. Available online: http://www.tech4effect.eu/wp-content/uploads/2019/11/manual-english-v13-201909.pdf (accessed 25th Jan 2021).

Erber, G., Stelzer, S., Stampfer, K., 2021: Evaluation of a novel mobile device app for value-maximized bucking by chainsaw. Int. J. of For. Eng. 32(sup1): 63–73. https://doi.org/10.1080/14942119.2021.1927362

Faaland, B., Briggs, D., 1984: Log bucking and lumber manufacturing using dynamic programming. Manage. Sci. 30(2): 245–257. https://doi.org/10.1287/mnsc.30.2.245

Garland, J., Sessions, J., Olsen, E.D., 1989: Manufacturing logs with computer-aided bucking at the stump. For. Pro. J. 39(3): 63–66.

Garlipp, T., 2018: edci: Edge Detection and Clustering in Images, R package version 1.1-3. Available online: https://CRAN.R-project.org/package=edci (accessed 25th Jan 2021).

Geerts, J.M., Twaddle, A.A., 1984: A method to assess log value loss caused by crosscutting practice on the skidsite. N. Z. J. For. 29(2): 173–184.

Gollob, C., Ritter, T., Nothdurft, A., 2020: Forest inventory with long range and high-speed personal laser scanning (PLS) and simultaneous localization and mapping (SLAM) technology. Remote Sens. 12(9): 1509. https://doi.org/10.3390/rs12091509

Gollob, C., Ritter, T., Wassermann, C., Nothdurft, A., 2019: Influence of scanner position and plot size on the accuracy of tree detection and diameter estimation using terrestrial laser scanning on forest inventory plots. Remote Sens. 11(13): 1602. https://doi.org/10.3390/rs11131602

Hyyppä, E., Kukko, A., Kaijaluoto, R., White, J.C., Wulder, M.A., Pyörälä, J., Liang, X., Yu, X., Wang, Y., Kaartinen, H., Virtanen, J-H., Hyyppä, J., 2020: Accurate derivation of stem curve and volume using backpack mobile laser scanning. ISPRS J. Photogramm. 161: 246–262. https://doi.org/10.1016/j.isprsjprs.2020.01.018

Hunčaga, M., Chudá, J., Tomaštík, J., Slámová, M., Koreň, M., Chudý, F., 2020: The Comparison of Stem Curve Accuracy Determined from Point Clouds Acquired by Different Terrestrial Remote Sensing Methods. Remote Sens. 12(17): 2739. https://doi.org/10.3390/rs12172739

Keefe, R.F., Wempe, A.M., Becker, R.M., Zimbelman, E.G. Nagler, E.S., Gilbert, S.L., Caudill, C.C., 2019: Positioning methods and the use of location and activity data in forests. Forests 10(5): 458. https://doi.org/10.3390/f10050458

Kivinen, V-P., 2007: Design and testing of stand-specific bucking instructions for use on modern cut-to-length harvesters. Doctoral thesis. University of Helsinki, Helsinki (Finland), 27th Apr.

Kovácsová, P., Antalová, M., 2010: Precision forestry – definition and technologies. Sumar. list 134(11–12): 603–610.

Kremser, P., (Waldgut Feistritz, Staudacher & Co Holzverwertung KG, Soboth, Austria). Personal communication, 2020.

Kublin, E., Breidenbach, J., Kändler, G., 2013: A flexible stem taper and volume prediction method based on mixed-effects B-spline regression. Eur. J. Forest Res. 132(5): 983–997. https://doi.org/10.1007/s10342-013-0715-0

Kublin, E., Breidenbach, J., 2013: TapeR: Flexible tree taper curves based on semiparametric mixed models. R package version 0.3.3. Available online: http://cran.r-project.org/web/packages/TapeR/ (accessed 25th Jan 2021).

Labelle, E.R., Bergen, M., Windisch, J., 2017: The effect of quality bucking and automatic bucking on harvesting productivity and product recovery in a pine-dominated stand. Eur. J. For. Res. 136(4): 639–652. https://doi.org/10.1007/s10342-017-1061-4

Laroze, A.J., Greber, B.J., 1997: Using Tabu Search to generate stand-level, rule-based bucking patterns. For. Sci. 43(2): 157–169. https://doi.org/10.1093/forestscience/43.2.157

Laroze, A.J., 1999: A linear programming, Tabu Search method for solving forest-level bucking optimization problems. For. Sci. 45(1): 108–116. https://doi.org/10.1093/forestscience/45.1.108

Liang, X., Kankare, V., Yu, X., Hyyppä, J., Holopainen, M., 2014: Automated stem curve measurement using terrestrial laser scanning. IEEE Trans. Geosci. Remote. Sens. 52(3): 1739–1748. https://doi.org/10.1109/TGRS.2013.2253783

Liang, X., Hyyppä, J., Kaartinen, H., Lehtomäki, M., Pyörälä, J., Pfeifer, N., Holopainen, M, Brolly, G., Pirotti, F., Hackenberg, J., Huang, H, Jo, H.-W., Katoh, M., Liu, L., Mokroš, M., Morel, J., Olofsson, K., Poveda-Lopez, J., Trochta, J., Wang, D., Wang, J., Xi, Z., Yang, B., Zheng, G., Kankare, V., Luoma, V., Yu, X, Chen, L., Vastaranta, M., Saarinen, N., Wang, Y., 2018: International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. 144: 137–179. https://doi.org/10.1016/j.isprsjprs.2018.06.021

Müller, C.H., Garlipp, T., 2005: Simple consistent cluster methods based on redescending M-estimators with an application to edge identification in images. J. Multivar. Anal. 92(2): 359–385. https://doi.org/10.1016/j.jmva.2003.12.005

Näsberg, M., 1985: Mathematical programming models for optimal log bucking. Doctoral thesis. Linköping University, Linköping (Sweden).

Olsen, E.D., Pilkerton, S., Garland, J., Sessions, J., 1991: Questions about optimal bucking. Forestry Research Lab, Oregon State University, Corvallis (OR, U.S.A), 18 p.

Olsen, E., Stringham, B., Pilkerton, S., 1997: Optimal bucking: Two trials with commercial OSU BUCK software. Foresty Research Lab, Oregon State University, Corvallis (OR, U.S.A), 32 p.

Pickens, J.B., Lyon, G.W., Lee, A., Frayer, W.E., 1993: HW-BUCK: A computer game for improving hardwood log bucking skills. J. For .91(8): 42–45.

Pierzchała, M., Giguère, P., Astrup, R., 2018: Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. Agr. 145: 217–225. https://doi.org/10.1016/j.compag.2017.12.034

Pnevmaticos, S.M., Mann, S.H., 1972: Dynamic programming in tree bucking. For. Prod. J. 22(2): 26–30.

Puumalainen, J., 1998: Optimal cross‐cutting and sensitivity analysis for various log dimension constraints by using dynamic programming approach. Scand. J. For. Res. 13(1–4): 74–82. https://doi.org/10.1080/02827589809382964

R Core Team, 2018: R: A language and environment for statistical computing. [accessed 2020 Sep 30]. R Foundation for Statistical Computing, Vienna (Austria). Available online: https://www.R-project.org/ (accessed 25th Jan 2021).

Ritter, T., Schwarz, M., Tockner, A., Leisch, F., Nothdurft, A., 2017: Automatic mapping of forest stands based on three-dimensional point clouds derived from terrestrial laser-scanning. Forests 8(8): 265. https://doi.org/10.3390/f8080265

Rossmann, J., Schluse, M., Schlette, C., 2010: The virtual forest: robotics and simulation technology as the basis for new approaches to the biological and the technical production in the forest. Syst. Cybernet. Inform. 8(5): 43–48.

Sessions, J., Layton, R., Guangda, L., 1988: Improving tree bucking decisions: A network approach. The Compiler 6(1): 5–9.

Sessions, J., Garland, J., Olsen, E.D., 1989: Testing computer-aided bucking at the stump. J. For. 82(4): 43–46. https://doi.org/10.1093/jof/87.4.43

Smith, J., Harrell, G., 1961: Linear programming in log production. For. Prod. J. 11(1): 8–11.

Talbot, B., Pierzchała, M., Rasmus, A., 2017: Applications of remote and proximal sensing for improved precision in forest operations. Cro. J. For. Eng. 38(2): 327–336.

Vaaja, M.T., Virtanen, J.-P-, Kurkela, M., Lehtola, V., Hyyppä, J., Hyyppä, H., 2016: The effect of wind on tree stem parameter estimation using terrestrial laser scanning. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. III-8: 117–122. https://doi.org/10.5194/isprs-annals-III-8-117-2016

Wagner, T., 2019: Leistungsbericht 2018 – Industrie 4.0 für den Cluster Wald und Holz – Umsetzung zukunftweisender Innovationen im Kompetenzzentrum Wald und Holz 4.0; Lehr- und Versuchsforstamt Arnsberger Wald, Arnsberg, Germany, 71–75.

Wiener Börse AG, 2006: Österreichische Holzhandelsusancen 2006 [Austrian Timber Trade Guidelines 2006.; Wiener Börse AG, Vienna (Austria), 271 p.

© 2022 by the authors. Submitted for possible open access publication under the
terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Authors’ addresses:

Gernot Erber, PhD *

e-mail: gernot.erber@boku.ac.at

Prof. Karl Stampfer, PhD

e-mail: karl.stampfer@boku.ac.at

University of Natural Resources and Life Sciences, Vienna

Department of Forest and Soil Sciences

Institute of Forest Engineering

Peter Jordan Strasse 82

1190, Vienna

AUSTRIA

Christoph Gollob, MSc

e-mail: christoph.gollob@boku.ac.at

Ralf Kraßnitzer, MSc

e-mail: ralf.krassnitzer@boku.ac.at

Prof. Arne Nothdurft, PhD

e-mail: arne.nothdurft@boku.ac.at

University of Natural Resources and Life Sciences, Vienna

Department of Forest and Soil Sciences

Institute of Forest Growth

Peter Jordan Strasse 82

1190, Vienna

AUSTRIA

* Corresponding author

Received: March 10, 2021

Accepted: April 22, 2021

Original scientific paper