Breakeven Analysis Considering Ultra-Fast Charging Stations at Mills for Battery-Electric Log Trucks

Range is a primary issue regarding the adoption of battery-electric vehicles. In-shift charging offers an alternative to extending range without the need for a heavier, more expensive battery. This paper recognizes that daily log truck productivity is a result of a small number of discrete events (loads delivered to a demand point). Delays such as in-shift charging become very important if they result in a lost load. If n is the number of loads a truck can deliver in a day without delays from in-shift charging, then the expected number of loads a truck can deliver with in-shift charging delays is n-1 + prob, where prob is the probability of completing the last load. The choice between a larger battery capable of a full day’s operation and a smaller battery that requires in-shift charging is formulated as a breakeven problem. Solving for the value of prob where the net revenue earned by the larger battery truck is equal to the net revenue earned by the smaller battery truck provides a battery size decision-point. Conducting a sensitivity analysis, the three factors that had the greatest impact on battery size selection were the hauling rate ($/tonne), the difference in net load, and the difference in depreciation cost between the large and small battery trucks.

Breakeven Analysis Considering Ultra-Fast Charging Stations at Mills for Battery-Electric Log Trucks

John Sessions, C. Kevin Lyons, David Hamilton

Abstract

Range is a primary issue regarding the adoption of battery-electric vehicles. In-shift charging offers an alternative to extending range without the need for a heavier, more expensive battery. This paper recognizes that daily log truck productivity is a result of a small number of discrete events (loads delivered to a demand point). Delays such as in-shift charging become very important if they result in a lost load. If n is the number of loads a truck can deliver in a day without delays from in-shift charging, then the expected number of loads a truck can deliver with in-shift charging delays is n-1 + prob, where prob is the probability of completing the last load. The choice between a larger battery capable of a full day's operation and a smaller battery that requires in-shift charging is formulated as a breakeven problem. Solving for the value of prob where the net revenue earned by the larger battery truck is equal to the net revenue earned by the smaller battery truck provides a battery size decision-point. Conducting a sensitivity analysis, the three factors that had the greatest impact on battery size selection were the hauling rate ($/tonne), the difference in net load, and the difference in depreciation cost between the large and small battery trucks.

Keywords: electric vehicles, heavy truck transport, break-even analysis

1. Introduction

Range is the primary issue regarding the adoption of battery electric vehicles. Recently, a number of heavy truck (Class 8) manufacturers have developed battery-electric truck tractors that are capable of being deployed in the logging industry. These include Kenworth (Kenworth 2022), Peterbilt (Peterbilt 2022), Freightliner (Freightliner 2022), Volvo (Volvo 2022), and Scania (Scania 2022). All have a two-speed transmission that can provide the necessary torque for mountainous operation. Current models have battery packs with 300–500 kWh capacity for short-range applications. A case study estimated that up to 1000 kWh would be required for full day operation of a battery-electric log truck operating in mountainous conditions, when including energy recovery through regenerative braking (Sessions and Lyons 2019).

Current practice in the logging industry is to fuel the truck once per day, usually off-shift. For diesel log trucks in Oregon and Washington, this requires about 0.304 tonnes of fuel per day (Mason et al. 2008). An equivalent lithium-ion battery might weigh 4–5 tonnes (Hunter et al. 2021). Thus, storing energy in liquid fuels or batteries is not a one for one trade, and this paper will consider two battery size options. There has been interest in establishing charging stations along interstate highways to take advantage of using smaller batteries that could reduce battery weight (Burke 2022). Studies suggest that battery-electric heavy trucks will be less costly than diesel trucks by 2030 (Hunter et al. 2021 and Burke 2022). It is suggested that in-shift charging of smaller battery-electric heavy trucks is more cost efficient than larger battery-electric heavy trucks (Burke 2022).

To charge a battery suitable for heavy trucks requires a high-power charger discharging direct current (Level 3) as compared to the smaller alternating current chargers (Level 2) that are used for many passenger cars. Currently, Level 3 chargers are in the range of 50–350 kW, but 500 kW are now being deployed (Doll 2022). A level 3 charging station costs several hundred thousand US dollars (Burke 2022).

It is common for a log truck to pick up a load of logs in the forest and deliver this to a mill (processing facility). The truck makes several trips per day, often to the same mill. Since mills are the destination for log trucks, they would be a potential location for an ultra-fast charging station where charging could be 500 kW at voltages of 400 or 800 volts. Large trucking companies or integrated forest industries are more likely to make an investment in this new technology. In this paper, we introduce a decision-making framework for a mill with its own logging trucks to compare purchasing a battery-electric truck for log transport with a smaller battery and charging at the mill during the day, to the alternative of purchasing a larger battery that does not require charging during the shift. The economic issues are battery cost, battery capacity (kWh), battery weight (tonnes), net vehicle weight available for cargo (tonnes), in-shift time required for charging, and charging station investment. The battery can be the single largest cost for the battery-electric truck, and this combined with battery weight limits the maximum size of the battery in Class 8 vehicles. Alternatively, if in-shift charging time is significant, this could reduce the number of trips the truck can make in a day, and this limits the minimum size of the battery.

2. Materials and Methods

We assume that a mill has at least part of its fleet with battery-electric log trucks under two scenarios:

Scenario 1: Each of the battery-electric log trucks has a large battery with sufficient charge capacity so that in-shift charging is not required.

Scenario 2: Each of the battery-electric log trucks has a smaller battery that must be charged at least once per day in-shift and the remainder out-of-shift.

We assume that the truck fleet operates as a profit center, maximizing net revenue per truck per day. The tradeoffs between a truck with a battery of sufficient capacity to run all day and recharge off-shift as compared to a truck with a smaller battery that must recharge in-shift are:

the larger battery is more expensive and heavier, reducing the weight of logs (tonnes) per load

the smaller battery requires in-shift charging time, which may preclude getting the last load of the day.

As a first approximation, the net revenue per day for the truck with the large battery is:

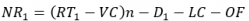 (1)

The net revenue for the truck with the small battery is:

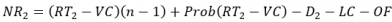 (2)

Where:

NRi the net revenue per day for truck type i, USD

R the trucking rate per tonne hauled, USD/tonne

Ti the load weight for truck type i, tonnes

VC the variable costs for operation and maintenance, tires, recharging, USD/trip (assumed the same for both truck configurations)

Di the depreciation for truck type i, USD/day

LC the labor cost per day (USD/day) assuming that the truck driver is working the same length day in each scenario

OF the other fixed costs for licenses, permits, insurance, property tax, USD/day

n the number of trips per day that are possible without in-shift charging

Prob the probability of completing the last load of the day when using a smaller battery and in-shift charging.

Depreciation and labor costs are considered fixed costs, which vary by the truck type. Property taxes, insurance, licenses are grouped under Other Fixed Costs. All other costs are lumped in variable costs including operating and maintenance costs, tires, and electricity cost. Electricity costs include the charging infrastructure.

Due to in-shift time required to recharge the smaller battery, we seek to identify the minimum probability of achieving the last load of the day that would make the net revenue between the truck with larger battery equal to the net revenue of the truck with the smaller battery. We assume that the variable costs, labor costs, and other fixed costs of the two truck options are the same and examine the impacts of those assumptions in the sensitivity analysis.

Setting NR1=NR2, and simplifying:

 (3)

We solve for the breakeven probability of achieving the last load per day using the truck with the smaller battery as

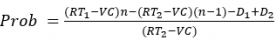 (4)

The National Renewable Energy Laboratory (NREL) evaluated alternative renewable energy heavy truck powertrains including compressed natural gas, hybrid-electric diesel, plug-in hybrid-electric vehicles, battery-electric, and fuel cell-electric power trains (Hunter et al. 2021). Their evaluation suggested that by 2025 battery-electric would be competitive with the lowest cost alternatives for single-shift weight-limited scenarios, and by 2050 it would be the lowest cost alternative. The NREL study estimated that battery- electric trucks were less competitive for multi-shift operations where trucks must be recharged during the shift. For our analysis, the purchase price and battery weight estimates provided by NREL will be used (Hunter et al. 2021). Short et al. (2022) estimate the average annual kWh per heavy tractor-trailer combination in the US to be 142,688 kWh, and for a 200-day work year, this results in 713 kWh/day. Given unpaved logging roads have higher rolling resistance and steeper grades than paved public highways, and that log loads do not usually have fairings to reduce drag, the kWh/day for a log truck could be higher than the US average heavy tractor-trailer combination. Sessions and Lyons (2019) conducted a case study that estimated battery capacity required for log trucks in mountainous terrain. Drawing from their case study, it can be assumed that 900 kWh is required for full day operation (100 km one-way trip, three times a day). Thus, the NREL 1173 kWh battery is used to simulate the truck requiring only off-shift charging and the 682 kWh battery as the option to charge, at least partially, in-shift (Table 1).

Table 1 Battery-electric truck inputs and financial data (Hunter et al. 2021).

Short and Crownover (2022) compare a class 8 sleeper cab truck with an internal combustion engine (ICE) to a battery electric vehicle (BEV). The battery used in the BEV version is large (7.7 tonnes). Using the truck weight values suggested by Short and Crownover (2022) and the small battery option considered in this paper, results in the ICE tractor weighing 8.3 tonnes and the BEV tractor weighing 9.9 tonnes. Given the rapid changes in battery technology, the 1.6 tonne difference between these two options is relatively small.

An average gross vehicle weight of 40 tonnes (Table 2) is used, which is the maximum gross vehicle weight typically permitted for a six-axle truck/trailer in Washington and Oregon (Mason et al. 2008). The net log load will depend upon the weight of the truck tractor and trailer. For the Washington study, the average largest legal load for the truck configurations surveyed was 26.7 tonnes. We assume that the powertrain for the truck with smaller battery will have the same weight as the powertrain for the diesel truck, 3.1 tonnes (engine, drivetrain, diesel fuel, fuel tanks), and that the larger battery truck will result in a reduced log load of 2.2 tonnes due to battery weight (5.3–3.1 from Table 1).

Table 2 Log truck survey data for state of Washington, USA (Mason et al. 2008)

In the following, we use local data to estimate starting values for a sensitivity analysis. Mason et al. (2008) found that the cost of owning and operating a log truck for a multi-truck company was $212,000 (equivalent to $288,000 in February 2023). We assume, on average, that companies must recover their costs for a sustainable industry. Back calculating at 3 trips per day, 40 weeks per year yields $18 per tonne [$288,000/(3 x 26.7 x 200 days)].

In our simulations for the battery-electric trucks, a 7% discount rate (real) (Hunter et al. 2021) is used for calculating equivalent annual costs for straight-line depreciation and a 7-year life. Since we are only interested in the difference between depreciation rates, and the difference is due to battery cost, zero percent salvage is assumed due to technological obsolescence. Public incentives for battery electric truck adoption were not considered. The difference in the purchase price between the truck with the large battery and the small battery is $93,000 (i.e. the difference in cost presented in Table 1). The equivalent annual cost at 7% discount rate is $17,256 or $86.3 per day. The equivalent annual cost is calculated as annual capital recovery for a uniform series of terminating payments (Bierman and Smidt 1984).

Variable costs consist of electricity plus charging infrastructure, truck maintenance, and tires (Table 3). We assume that the ultra-fast DC charging station at a mill could provide 500 kW at 800 volts and that a charging location area was available. To identify if this was feasible in western Oregon and western Washington, nine major mills were surveyed. Our mill survey identified that adequate power was available, and identified an electricity cost of $0.04–0.06 per kWh as the industrial rate at these sites. From the literature, a 500 kW ultra-fast DC charger, including infrastructure and installation would cost about $500,000, or about $1000 investment per kW of charging capacity (Evadoption 2021). The cost of electricity for charging is the sum of the electricity to the charger and the cost of the charger prorated over the number of kWh per year. We assume that the charger is being used 30% of each trucking day or 7.2 hours per day at 500 kW for 720,000 kWh per year. The equivalent annual cost of the $500,000 charging station investment (7 percent real discount rate, 7-year life) is $92,777. Thus the cost of electricity to the truck is the cost to the electricity supplied to the charger ($0.05 per kWh) plus the cost of the charger, $0.13/kWh ($92,777/720,000 kWh), for a total of $0.18 per kWh. This is equivalent to $54.00 per trip (900 kWh/3 x $.18/kWh), or $13.5 per hour (4 hours per trip). Other variable costs considered are operation and maintenance of $9.75/hr (Hunter el al. 2021), and tire costs of $3.79/hr ($9100/year inflation adjusted from (Conrad 2018) divided by 2400 hr/yr) for a total of $27.04/hr or $108.16 per trip.

Table 3 Variable costs for base scenario

3. Results

Substitute R = 18.0, T1 = 24.5, T2 = 26.7, VC = 108.2, n = 3, and D1 – D2 = 86.3 into Eq. 4, then the breakeven probability is 0.44. Thus, if the probability of completing the third load of the day is greater than 0.44, the truck with the smaller battery has a higher daily revenue than the large battery truck. If the probability of completing the last load is less than 0.44, the truck with the larger battery has a higher daily revenue.

To evaluate the sensitivity of the breakeven probability to the input parameters, selected input parameters were changed from their base values by multiplying the base value by 1.25 (+25%) or by 0.75 (–25%) holding all other inputs constant. For a 25% change in parameters, the breakeven probability was most sensitive to truck revenue per unit of logs and change in net load due to the difference in battery weights (Table 1), and least sensitive to discount rate, charging station cost, and charging station utilization (Table 4). Explanations for the directions of the changes are as follows:

increasing the revenue per tonne increased the breakeven probability. This result is due to the combined effects of the difference in payload between the large and small battery trucks, and the value of the small battery truck hauling the last load

increasing the difference between the log load for the large and small battery trucks (T2–T1) reduced the breakeven probability because increasing the difference in payloads reduces the effect of hauling one less load with the small battery truck

increasing the difference in depreciation cost (D1–D2) for the truck with the larger battery reduced the breakeven probability as the larger battery investment increased its cost

increasing the variable cost has a similar effect to reducing the truck revenue. Increasing the variable cost reduced the net truck revenue for a load, and for the smaller truck, this reduces the penalty for missing the last load, thus, the breakeven probability decreases

increasing life of the truck and the charging station reduces fixed costs, which favors the larger battery and increases the breakeven probability

increasing the cost of the charging station increases variable costs, which has the opposite effect as increasing charging station utilization and slightly favors the smaller battery and reduces the breakeven probability.

Table 4 Sensitivity of breakeven probability to 25% change in selected parameters using Eq. 4

4. Discussion

500 kW chargers have been used in this analysis. These chargers are in early stages of deployment but they are expected to be widely available by 2025 (Doll 2022). Although cost of electricity in Oregon and Washington is low, the cost of charging infrastructure can significantly increase the final cost. We have made assumptions about the charging infrastructure and provided some insight into the sensitivity of the breakeven probability to those assumptions. Change in charging station utilization can also affect the results. The scenarios considered in this paper placed all charging at the mill, both in-shift and off-shift. Other scenarios are possible, for example, off-shift charging off-site. This would decrease utilization of the charger at the mill, increasing electricity costs for that portion of the electricity budget. Off-site charging might also be at a higher cost than the industrial rates observed from our mill survey. We have assumed that the battery is an integral part of the truck, i.e., it is not removed during charging. An alternative model is being deployed in China (Xiao 2022) and Australia (Janus Electric 2023), where three tonne batteries are being swapped at recharge time in only a couple of minutes. This requires a truck design where the battery is designed to be easily removed, such as between the cab and safety rack. The upside of the battery swap model, if applied to our problem, is that the probability of completing the last load would approach 1.0. Important considerations in the battery swap model are the availability of the battery swappable truck designs, the ratio of batteries per fleet to trucks per fleet, and the cost of the swapping/recharging station.

Formulating this problem as the breakeven probability where the net revenue for the large battery option equals that of the small battery option will be useful for truck fleet managers. Many factors affect the number of loads per day a log truck can deliver, and these factors are continually changing. The distance between the pickup and delivery points varies regularly as the logging operation moves to different units. The time to travel a route can change with weather conditions. The time to load the truck depends on the size of the logs being loaded. Delays waiting to be loaded and unloaded can be a function of mechanical breakdowns and congestion with multiple trucks competing for access. The truck manager has the option to send trucks on longer or shorter routes, and by managing these choices, is able to mitigate the risk of losing a load on a particular day. Methods such as Monte Carlo simulation, where parameter values are selected from distributions, could be very useful for estimating the probability of making the final load of the day in a particular operation. This probability could be compared to the breakeven probability for the large or small battery option (in-shift charging or off-shift only charging). If the probability of making the last load of the day was greater than the breakeven probability, then the preferred choice would be the smaller battery and in-shift charging.

If the probability of making the last load with the smaller battery scenarios were larger than the breakeven probability, but less than 1.0, then truck productivity (tonnes/day) would be lower than the larger battery option. This would require a larger fleet with additional drivers. These potential impacts were not considered in this study. The sensitivity analysis considered the effects of a 25% change in selected parameters holding all other factors constant. Sometimes financial factors are correlated, for example, revenue, cost, and discount rate changes. These factors could then be grouped into low cost, medium cost, and high-cost scenarios. We chose to vary factors one at a time to isolate their individual effects, but grouping factors might provide additional insight. This study did not include the effects of taxes and subsidies. Taxes or subsidies that favor one scenario above another could affect the breakeven probability.

5. Conclusions

This paper conducted a sensitivity analysis considering factors that affected the breakeven probability of completing the last load of the day when using in-shift charging. Three factors that had the greatest impact were hauling rate ($/tonne), and the difference in net load and in depreciation cost between the large and small battery trucks. Increasing the hauling rate results in a higher breakeven probability, while increasing the difference in net load and depreciation reduced the breakeven probability. These differing results highlight that the decision on whether to use in-shift charging must be made in the local context. The local context includes straight forward parameter values such as energy cost and haul rates, but also understanding the local hauling options and how these can be manipulated in order to maximize the likelihood of completing the last load of the day when in-shift charging. The methods presented in this paper allow managers to use their own judgement to game the probability values and to consider which option (large or small battery) provides them the best opportunity for success.

Future work includes considering battery swapping and charging station utilization. Swapping batteries rather than delaying the truck during in-shift battery charging is an alternative strategy. The battery swap model permits use of a smaller battery, lower truck investment, and reduced in-shift charging time. This would require an alternative truck design for the North American market. Our estimate of charging station utilization needs additional study. The more trucks that can share the same charger, the lower the recharging cost per unit of energy. Dispatching trucks to reduce waiting time at the charging stations will be important. Discrete simulation of the truck fleet could improve estimates of truck workload (kWh per day) and driver waiting time.

We have not considered the charging station management model. Possible models might be an entity that manages charging stations at several mills, a charging station managed by a mill or the owner of several mills, or a charging station operator that manages both industrial charging at mills and commercial charging off-site. Future work should include discrete simulation of truck operations to better understand truck workloads, queuing times at the charging station, and evaluation of different business models.

6. References

Burke, A., 2022: Assessment of Costs and Benefits of Providing Charging Facilities for Battery-Electric Heavy-Duty Trucks at Safety Roadside Areas. Available online at https://escholarship.org/uc/item/3c07s2jh. Last accessed February 7, 2023

Bierman, H., Smidt, S. Jr., 1984: The Capital Budgeting Decision. Sixth Edition. Macmillan Publishing, NY, 548 p.

Conrad, J., 2018: Costs and Challenges of Log Truck Transportation in Georgia, USA. Forests 9(10): 650. https://doi.org/10.3390/f9100650

Doll, S., 2022: NIO Power Day 2022: New 500 kW fast chargers coming to China and the EU this year. Available online: https://electrek.co/2022/07/06/nio-power-day-2022/. Last accessed February 7, 2023

Evadoption, 2021: How Many EV Charging Stations Will $10 Billion Buy for America? Available online: https://evadoption.com/how-many-ev-charging-stations-will-10-billion-buy-for-america/. Last accessed February 7, 2023

Freightliner, 2022: Freightliner eCascadia. Available online: https://freightliner.com/trucks/ecascadia/specifications/. Last accessed December 24, 2022

Hunter, C., Penev, M., Reznicek, E., Lustbader, J., Birky, A., Zhang, C., 2021: Spatial and Temporal Analysis of the Total Cost of Ownership for Class 8 Tractors and Class 4 Parcel Delivery Trucks. Golden, CO: National Renewable Energy Laboratory. NREL/TP-5400-71796. Available online: https://www.nrel.gov/docs/fy21osti/71796.pdf. Last accessed February 7, 2023

Janis Electric, 2023: Electrifying Australia's road transport fleet with tomorrows technology, today. Available online: https://www.januselectric.com.au/. Last accessed June 13, 2023

Kenworth 2022: T680E Specifications. Available online: https://www.kenworth.com/media/qm5ly0sm/t680e-05-16-2022.pdf. Last accessed December 24, 2022

Mason, C.L., Casavant, K., Lippke, B., Nguyen, D., Jessup, E., 2008: The Washington Log Trucking Industry: Costs and Safety Analysis. Rural Technology Initiative College of Forest Resources University of Washington. 111 p. Available online: https://www.ruraltech.org/pubs/reports/2008/log_trucks/log_truck_report.pdf. Last accessed February 7, 2023

Peterbilt, 2022: Electric Vehicles. Available online: https://www.peterbilt.com/electric-vehicles. Last accessed December 24, 2022

Scania, 2022: Scania introduces electric trucks for regional long haul. Available online at https://www.scania.com/group/en/home/newsroom/press-releases/press-release-detail-page.html/4286998-scania-introduces-electric-trucks-for-regional-long-haul. Last accessed December 24, 2022

Sessions, J. Lyons, K., 2019: Harvesting elevation potential from mountain forests. International J. of Forest Engineering 29(3): 192–198. https://doi.org/10.1080/14942119.2018.1527173

Short, J., Crownover, D., 2022: Understanding the CO2 impacts of zero-emission trucks. Available online: https://truckingresearch.org/wp-content/uploads/2022/05/ATRI-Understanding-CO2-Impacts-of-Zero-Emission-Trucks-May-2022.pdf. Last accessed June 8, 2023

Short, J., Shirk, A., Pupillo, A., 2022: Charging infrastructure challenges for the US electric vehicle fleet Available online: https://truckingresearch.org/2022/12/new-atri-research-evaluates-charging-infrastructure-challenges-for-the-u-s-electric-vehicle-fleet/. Last accessed June 8, 2023

Volvo, 2022: The Volvo VNR electric. Available online: https://www.volvotrucks.us/trucks/vnr-electric/. Last accessed December 24, 2022

Xiao, Y., 2022: China's First Highway Battery Swap Service for Heavy-Duty Trucks Get Going. Available online: https://www.yicaiglobal.com/news/china-first-highway-heavy-duty-truck-battery-swap-service-starts-operating. Last accessed November 26, 2022

© 2023 by the authors. Submitted for possible open access publication under the
terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Authors' addresses:

Prof. John Sessions, PhD

e-mail: john.sessions@oregonstate.edu

Assoc. Prof. Kevin C. Lyons, PhD *

e-mail: keivn.lyons@oregonstate.edu

David Hamilton, MSc

e-mail: david.hamilton@oregonstate.edu

Oregon State University

Dept. of Forest Engineering, Resources and Management

97331 Corvallis, Oregon

USA

* Corresponding author

Received: March 07, 2023

Accepted: June 16, 2023

Original scientific paper