Double Bark Thickness Estimation Models of Common European Broadleaved Species for Harvester Timber Volume Estimation in Czechia

The share of the annual volume of harvester-produced timber in Czech forest bioeconomy has increased in the last decades. To estimate under-bark timber volume, harvester systems allow choosing between two different bark deduction models – diameter band (DBM) and linear model. However, linear models were not calibrated for the conditions of Czech forestry. Therefore, the objective of this research was to develop, for local conditions in Czechia, linear functions for estimating the double bark thickness of two groups of broadleaved species (beech and oak) and to test their viability based on real harvest data. To create the linear functions, official Czech cubing tables were used. Data from real harvests were gathered from fifteen harvesters. A sample containing 4995 logs belonging to the beech group was analyzed using descriptive statistics and the Paired Wilcoxon tests. The mean double bark thickness for beech group was 15.1 mm (polynomial and linear model). For oak group, it was 15.48 mm (polynomial) or 15.49 mm (linear). The results of real harvests for beech group revealed that the mean double bark thickness estimated by the polynomial function was 7.08 mm. The linear function estimates were closer to the value estimated by the polynomial (6.84 mm) than DBM estimates (6.68 mm). Therefore, we can state that the newly developed linear models can be used in fully mechanized harvesting instead of manual bark deduction methods in Czechia.

Double Bark Thickness Estimation Models of Common European Broadleaved Species for Harvester Timber Volume Estimation in Czechia

Martin Jankovský, Jiří Dvořák, Radim Löwe, Pavel Natov, Ondřej Nuhlíček

Abstract

The share of the annual volume of harvester-produced timber in Czech forest bioeconomy has increased in the last decades. To estimate under-bark timber volume, harvester systems allow choosing between two different bark deduction models – diameter band (DBM) and linear model. However, linear models were not calibrated for the conditions of Czech forestry. Therefore, the objective of this research was to develop, for local conditions in Czechia, linear functions for estimating the double bark thickness of two groups of broadleaved species (beech and oak) and to test their viability based on real harvest data. To create the linear functions, official Czech cubing tables were used. Data from real harvests were gathered from fifteen harvesters. A sample containing 4995 logs belonging to the beech group was analyzed using descriptive statistics and the Paired Wilcoxon tests. The mean double bark thickness for beech group was 15.1 mm (polynomial and linear model). For oak group, it was 15.48 mm (polynomial) or 15.49 mm (linear). The results of real harvests for beech group revealed that the mean double bark thickness estimated by the polynomial function was 7.08 mm. The linear function estimates were closer to the value estimated by the polynomial (6.84 mm) than DBM estimates (6.68 mm). Therefore, we can state that the newly developed linear models can be used in fully mechanized harvesting instead of manual bark deduction methods in Czechia.

Keywords: linear modeling, diameter band bark deduction model, beech under-bark volume estimation, oak under-bark volume estimation, non-wood forest products, forest bioeconomy

1. Introduction

The bark includes all tissues outside the cambium (Costa et al. 2021) and is vital for a tree survival during growth. It protects the tree against biotic (e.g. insects, fungi) and abiotic (e.g. weather, fire, physical damage) environmental factors (Jankovský et al. 2019). Its thickness and texture differ significantly from extremely rough to fine, depending on e.g. the tree species (West 2015) or the environment (Zeibig-Kichas et al. 2016). Certain tree species have rough bark (e.g. pine, oak), while others have fine bark (e.g. beech, plane tree, eucalyptus). For example, in areas with frequent forest fires, trees such as sequoias developed rough bark (Pausas 2015, Charles-Dominique et al. 2017). Trees with a rough bark have also vital tissue protection against attack from pathogens, herbivores, frost and drought (Costa et al. 2021). Studies performed on certain tree species have found that bark thickness varies according to their size, crown ratio, position within the canopy, height along the tree stem, genetic identity, latitude, etc. (Berrill et al. 2020).

The bark, as an integral part of every tree, also contributes to its total stem volume. Worldwide, about 363 million cubic meters of sawn timber is produced, with the volume of bark accounting for an estimated 10% of the total stem volume (Wehenkel et al. 2012). Miles and Smith (2009) revealed that the bark of more than 150 tree species in the United States represented from 12% to 15% of the total tree volume. Understanding how the thickness of tree bark varies within and among trees has practical application in forest science and management (Berrill et al. 2020), because bark thickness is an important variable in both forest mensuration and post-harvesting records (Muhairwe 2000).

In Central European countries, timber is measured over bark, but sold under bark. The bark is therefore provided to customers free of charge, and they can continue to use it and profit from it. With the development of technologies, estimates of bark volumes have become relevant for industries linked to forestry (Kozak and Yang 1981). Bark is widely used in soil amelioration, as ground cover (Wehenkel et al. 2012), or as an energy source, with the heating value of dry bark of ~ 18,000 kJ/kg (the same as wood), and the density of ~ 350 kg/m3 (Vaucher 2003). Therefore, most pulp and paper mills, plywood plants, and sawmills burn all their bark to produce energy to run the plant and to dry products (Bowyer et al. 2007). It is also used as a chemical feed stock (Sáenz-Esqueda et al. 2010).

Due to the existence of many factors affecting the bark thickness, the construction of a generic bark thickness estimation model is impossible. Therefore, double bark thickness estimation methods were developed for many tree species worldwide (Li and Weiskittel 2011). Czech foresters use bark deduction tables, based on a polynomial model developed by Wojnar (2007). This polynomial model is based on data from the Czech cubing tables (CCT) specified in the ČSN 48009 technical standard (ČSN 1977). There are also manual bark deduction procedures; however, they are laborious, time-consuming, error-prone, and are becoming obsolete, due to the increase of fully mechanized harvesting systems.

The share of the annual volume of Czech timber produced by harvesters has increased in the last decades – up to 38% in 2015 (Natov et al. 2017, Dvořák et al. 2019). Moreover, due to the high productivity of harvesters, their greater expansion in Czechia and other Central European countries can be expected (Sedmíková et al. 2020).

However, Wojnar’s (2007) polynomial bark deduction model cannot be used with harvesters, as the forest machine systems installed in harvesters are not equipped with such functionality. This is because all forest machine systems of harvesters use a unified standard – StanForD (Skogforsk 2012a). Based on the version of the StanForD standard implemented in the machines (StanForD classic or StanForD 2010), users can select from two (StanForD classic) or four (StanForD 2010) models for double bark thickness estimations.

The first model that can be chosen in the StanForD classic standard is the diameter band bark deduction model (DBM), where the double bark thickness deductions are based on the midspan diameter band to which a log relates. The second model is a linear function (Eq. 1), constructed for the Scandinavian conditions (Zacco 1974), and needs to be calibrated for use in the conditions of Czechia to improve the accuracy of the double bark thickness (DBT, mm) estimates, as in Australia for radiata pine (Strandgard and Walsh 2011). Aside from these, StanForD 2010 offers two more models for predicting the double bark thickness of Scots Pine and Norway Spruce – the multivariate linear model, incorporating the diameter at breast height as a second parameter, aside from midspan overbark diameter, and a more complex logistic model. We chose not to consider these two models in our study, as they relate to the new standard, which was not used in Czechia at the time of writing of this paper.

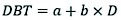(1)

Where:

a and b represent parameters

D stem diameter over bark, mm.

Therefore, the objective of this research was to develop, for local conditions in Czechia, a linear function for estimating the double bark thickness of broadleaved species, oak and beech, that will be compatible with harvester systems. Subsequently, we tested whether the linear function was suitable for practical use.

2. Materials and Methods

2.1 Czech Cubing Tables Dataset and the Polynomial Function

The Czech cubing tables (CCT) dataset specified in the ČSN 48009 technical standard (ČSN 1977) was used for developing the linear function for estimation of the double bark thickness of common broadleaved species. The CCT were designed in 1977 from a comprehensive dataset for each major tree species or groups of tree species with similar bark generation characteristics. The midspan diameters of logs were measured over bark, then debarked and remeasured. A table for each tree species or group of tree species contains information about the log lengths and the midspan diameters measured over bark to which the values of the under-bark volume are assigned. The Huber formula (Husch et al. 2003) was used (Eq. 2) for the estimation of volume under bark, VUB (m3):

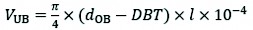(2)

Where:

dOB is midspan over-bark diameter, mm

DBT is double bark thickness, mm

l is log length, m.

To estimate the double bark thickness (DBT, mm) of tree species or groups of tree species, the CCT data can be expressed as a polynomial function (Eq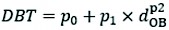. 3):

(3)

Where:

dOB is midspan over-bark diameter, mm

p0, p1 and p2 are parameters varied based on tree species or group of tree species.

This polynomial function with its parameters is also included in the Recommended Rules for Timber Measurement and Sorting in the Czech Republic 2008 (Wojnar 2007) and recommended for use in practical forestry.

This study was focused on common Czech broadleaved tree species. Based on the CCT, these species are broken down into two groups with similar bark characteristics. The first group – Oak – contains oak (Quercus sp.), elm (Ulmus sp.), ash (Fraxinus sp.), birch (Betula sp.), alder (Alnus sp.), willow (Salix sp.) and horse chesnut (Aesculum hippocastanum). The second group – Beech – contains beech (Fagus sylvatica), maple (Acer sp.), hornbeam (Carpinus betulus), rowan (Sorbus sp.), linden (Tilia sp.), poplar (Populus tremula), London planetree (Platanus acerifolia) and several others (Prunus domestica, Prunus avium, Malus domestica, Pyrus sp.). For each group, distinct parameters are used for estimations of double bark thickness (Table 1).

Table 1 Parameters of polynomial function used for double bark thickness estimations of groups of common broadleaved species in Czechia (ČSN 1977, Wojnar 2007)

2.2 Construction of Linear Function and Statistical Analysis

The two univariate linear functions (one for each species group), compatible with harvester forest machine systems, were fitted to the related CCT data using the least squares method. The outcome of the functions was the double bark thickness of the particular species group in mm.

To obtain the parameters of the linear functions, we calculated the under-bark diameters of logs using the Huber formula (Eq. 2) from the over-bark diameters, over- and under-bark volumes, and log lengths found in the CCT. The fit of the linear functions to the CCT data was tested through the mean absolute error (the average absolute difference between the values predicted by the linear models and the CCT values; MAE), mean absolute percentage error (the average absolute difference between the linearly modeled values and the CCT values divided by the CCT value, multiplied by 100; MAPE), root mean square error (the square root of the average of squared errors; RMSE), mean bias error (the average difference between the predicted values predicted through the linear models and the CCT values; MBE), and mean percentage error (the average difference between the values predicted by the linear models and the CCT values divided by the mean CCT double bark thickness, multiplied by 100; MPE). The procedure was described in more detail for Norway spruce by Jankovský et al. (2019).

2.3 Diameter Band Bark Deduction Model

Diameter band bark deduction model (DBM) is a bark deduction method which, in addition to the polynomial function, is recommended for use in practical forestry by Wojnar (2007). The DBM is also based on the CCT data (ČSN 1977). We used this method to compare the accuracy of the newly created linear functions with other options viable for use in harvester forest machine systems. Double bark thickness values in all ten diameter bands for each group of broadleaved tree species are shown in Table 2.

Table 2 Double bark thickness values for diameter band bark deduction model (DBM) in various diameter bands assigned to each group of broadleaved tree species, as assigned by Wojnar (2007)

2.4 STM Database and Statistical Analysis

Data were collected from harvested logs to test whether the linear function was comparable to the bark thickness estimations of the polynomial function (Wojnar 2007). Fifteen harvesters that carried out thinnings and final fellings throughout Czechia in 2016–2018 were used to gather the data. To ensure the accuracy of length and diameter measurements, a control measurement was performed using a digital caliper at the beginning of each work day and, if necessary, length and diameter gauges were calibrated in the harvester head of the machine (Skogforsk 2012a, Löwe et al. 2019). The forest machine systems of harvesters stored data on each processed stem in a separate STM file. Unfortunately, no trees belonging to the oak group were harvested. We could, therefore, only test the real-life accuracy of the linear function created for the beech group.

Due to the extensive size of the database (0.5 million STM files), we created a random sample containing 10% STM files. The PHP array_r- and() function (PHP.net 2019) was applied to create this random sample. After filtering the STM files to those belonging to the species under the beech group, a sample containing 4995 logs from 1162 stems was obtained. Over- and under-bark volumes of logs were estimated using the algorithm of M3toDE price type, based on Huber formula and rounding down the midspan diameter (Skogforsk 2012b, Löwe et al. 2019). For STM data analysis, we used MS Excel 365 and Tibco STATISTICA 13.0. Descriptive statistics were used to gain average and summary values of individual variables. The Kolmogorov-Smirnov test found the data were not normally distributed so Paired Wilcoxon tests were used to test differences between the values of double bark thickness estimations according the polynomial, linear and DBM model (each pair was tested individually). A significance level of α=5% was chosen for all statistical tests.

3. Results

Based on the CCT dataset, the linear function estimating the double bark thickness of both groups of common European broadleaved species was developed. The coefficients of newly developed linear function (Table 3) were set based on the fit parameters to the related values of the CCT dataset. The double bark thickness of the beech group ranged between 6 and 17.97 mm in the CCT, whereas the linear model yielded double bark thickness estimates between 5.69 and 18.71 mm. For the oak group, the CCT double bark thickness ranged between 17.39 and 51.35 mm, and the linear model yielded double bark thickness estimates between 17.25 and 50.85 mm. The mean double bark thickness for Beech was 12.76 mm (polynomial) or 12.20 mm (linear) and 34.07 mm (polynomial) or 34.05 mm (linear) for oak. The mean absolute percentage error between the new linear bark thickness estimation models and the current standard polynomial models was 6.38% for beech and 0.44% for oak. The mean absolute error of our model was 0.71 mm for beech and 0.15 mm for oak.

Table 3 Coefficients of newly developed linear function for Oak and Beech groups of common broadleaved species

Table 4 Parameters of fit of newly developed linear functions for Beech and Oak groups of common broadleaved species to related values of CCT dataset

In the graphic (Fig. 1), demonstrating the course of the double bark thickness of the linear function, the polynomial function and the DBM for the midspan diameters of logs in Oak group (Fig. 1a), the minimal difference between the newly developed linear function and polynomial function for oak is clearly visible. In Beech group (Fig. 1b), the curves of newly developed linear function and polynomial function show greater differences.

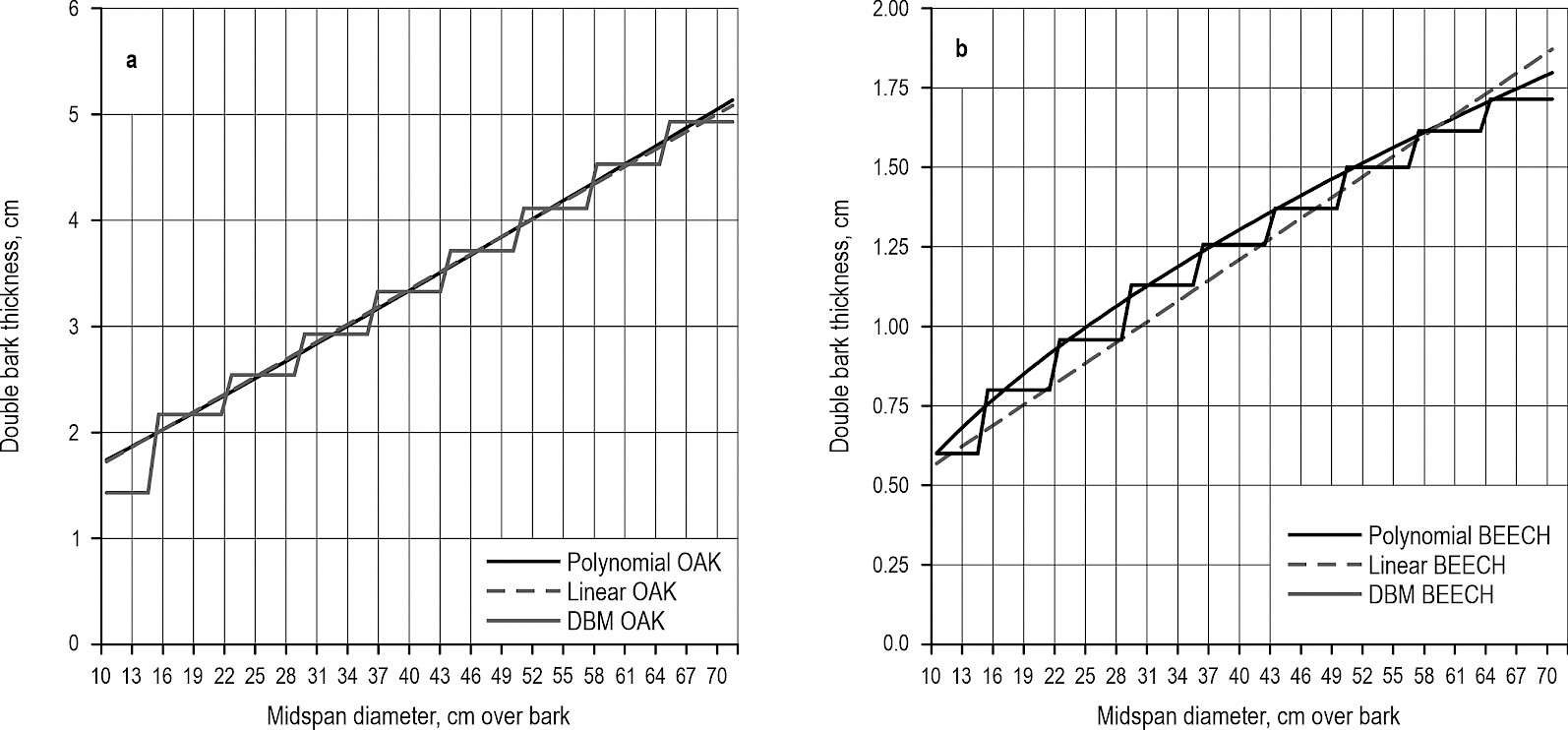
Fig. 1 Double bark thickness according to linear function, polynomial function and diameter band bark deduction model (DBM) for midspan diameters of logs in Oak group (Fig. 1a) and Beech group (Fig. 1b) of broadleaved tree species

The data from harvested beech logs, used to test differences between the values of double bark thickness estimations according to the polynomial, linear and DBM model, was represented by the following values of the variables: the mean overbark midspan diameter of a log was 153 mm (SD=standard deviation=75 mm), the mean total length of a log was 215 cm (SD=73 cm), the mean log over-bark volume was 0.05 m3 (SD=0.08 m3) and the sum of over-bark volumes of all logs was 257.12 m3. For these beech logs, the highest mean double bark thickness was obtained by the Polynomial function (7.08 mm; SD=1.9 mm), followed by the Linear function (6.84 mm; SD=1.6 mm) and the DBM (6.68 mm; 2.1 mm) (Fig. 2). Significant differences were revealed between the double bark thickness estimated by the Polynomial function and the Linear one (T=259818, Z=35.74, p<0.001), as well as by the DBM (T=3035465, Z=31.43, p<0.001). Significant differences were also found between the double bark thickness estimated by the Linear function and the DBM (T=5818524, Z=4.12, p<0.001).

When the double bark thicknesses estimated by the three bark deduction methods were used to calculate the total under-bark volume of all logs, the total volume was reduced to 234.46 m3 (by 8.8%) using the Polynomial function, to 235.35 m3 (by 8.5%) using the Linear function, and to 236.29 m3 (by 8.1%) using the DBM.

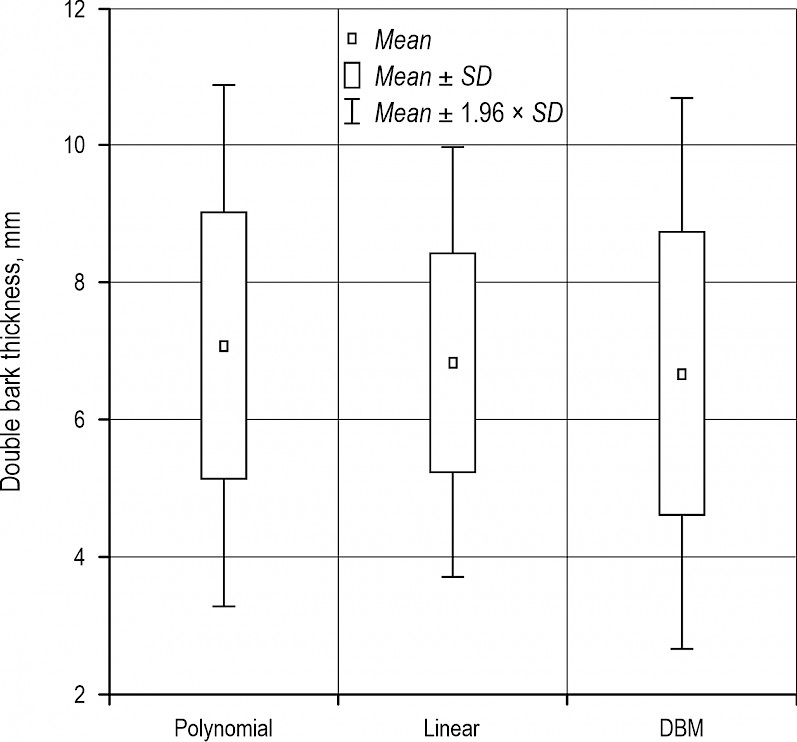
Fig. 2 Differences between mean double bark thickness estimations according to Linear function, Polynomial function and diameter band bark deduction model (DBM). Double bark thicknesses were estimated for harvested beech logs

4. Discussion and Conclusions

Currently, the DBM is used for deducting bark thickness in forest machine systems of Czech harvesters. This method is based on the CCT dataset (ČSN 1977). However, the disadvantage of this method is that constant double bark thickness values are used for relatively wide diameter bands (range 6–8cm). In addition, manually entering band deduction coefficients into the forest machine systems increases the risk of human error and increases the time consumption, compared to using a linear function, where only two coefficients need to be put in the forest machine systems.

Although we could not test our linear model developed for oak group on data from real harvests, looking at the curve of the linear function (Fig. 1a), it can be observed that the values of double bark thickness will differ very little from the values of the polynomial function. Nevertheless, in further research, it would be appropriate to verify the function using harvest data.

Testing the linear function for beech group revealed that the average double bark thickness was lower than the double bark thickness estimated by the polynomial model, but higher than estimated by the DBM. Although the results showed that there were statistically significant differences between the individual bark deduction methods, they were in fact negligible and using a linear function instead of the DBM for beech group seems more appropriate from a practical standpoint. The smallest under-bark volume was estimated using the polynomial function. The linear function overestimated the volume of merchantable by 0.3 percentage points compared to the polynomial function, and the DBM then by 0.7 pp. In the last decades, the goal of developed countries has been to make efficient use of renewable biological sources while ensuring their sustainable use. Forest bioeconomy is gaining momentum world-wide, including Czechia (Purwestri et al. 2018, Purwestri et al. 2020) and utilization and monetization of tree bark (Pásztory et al. 2016) is a key aspect of it. Therefore, we consider the development of new methods for determining the amount of bark of timber produced by harvester technology, usable in the growing conditions of Czechia, to be important also from the point of view of the forest bioeconomy.

That being said, bark deduction adds complexity to estimation of merchantable timber volume. Bark is a renewable raw material that can be used as fuel, landscaping product or, after composting, as a substrate for growing plants. Similarly to Czechia, official double bark thickness estimation methods are based on decades old datasets in many countries, as stated by Marshall et al. (2006), Strandgard and Walsh (2011) or Stängle et al. (2017). Therefore, we could consider whether it would be better to trade the timber according to the Finnish model (i.e. trade over bark) and avoid difficulties with the deduction of the bark.

In this research, linear functions for estimating the double bark thickness of broadleaved species, usable in harvester systems in local conditions of Czechia, were developed. The presented linear models can be used in fully mechanized harvesting instead of manual bark deduction. This would greatly help limiting the amount of time and labor consumed by foresters for remeasuring logs. It also limits the potential for human error, which will help not only large-scale forest owners but also small-scale forest owners, for whom manual estimation of the volume of merchantable timber presents a considerable burden.

Further research is required to test the accuracy of the bark deduction models by manually measuring the over bark diameter and double bark thickness of harvested oak and beech group logs and comparing double bark thickness values predicted using the polynomial, linear and DBM models.

Acknowledgments

The research described in this paper was supported by the National Agency for Agricultural Research Czech Republic under the projects no. QK1920391 called »Diversification of the influence of bioeconomy on strategic documents of the forestry and timber sector as a basis for state administration and proposal of strategic goals until 2030« and no. QK1920435 called »The improvement and support of communication, survey and management of outbreak and disaster situations as a tool for optimization of state administration in the forestry sector.«

6. References

Berrill, J.P., O’Hara, K.L., Kichas, N.E., 2020: Bark Thickness in Coast Redwood (Sequoia sempervirens (D.Don) Endl.) Varies According to Tree- and Crown Size, Stand Structure, Latitude and Genotype. Forests 11(6): 637. https://https://doi:10.3390/f11060637

Bowyer, J.L., Shmulsky, R., Haygreen, J.G., 2007: Forest products and wood science: An introduction, Ames, IA: Wiley-Blackwell, 504 p.

Charles-Dominique, T., Midgley, G.F., Bond, W.J., 2017: Fire frequency filters species by bark traits in a savanna-forest mosaic. J Veg Sci 28(4): 728–735. https://doi:10.1111/jvs.12528

Costa, E.A., Liesenberg, V., Finger, C.A.G., Hess, A.F., Schons, C.T., 2021: Understanding bark thickness variations for Araucaria angustifolia in southern Brazil. J For Res 32(3): 1077–1087. https://doi:10.1007/s11676-020-01163-1

ČSN, 1977: Standard n. 48 0009: Tabulky objemu kulatiny bez kůry podle středové tloušťky měřené v kůře (Tables of roundwood inside bark volume according to midspan diameter measured over bark). Prague, CZ: ČSN, 592 p.

Dvořák, J., Chytrý, M., Natov, P., Jankovský, M., Beljan, K., 2019: Long-term Cost Analysis of Mid-performance Harvesters in Czech Conditions. Austrian J For Sci 136(4): 351–372.

Husch, B., Beers, T.W., Kershaw, J.A.Jr., 2003: Forest Mensuration, 4th ed.; John Wiley and Sons: New York, NY, USA, 456 p.

Jankovský, M., Natov, P., Dvořák, J., Szala, L., 2019: Norway spruce bark thickness models based on log midspan diameter for use in mechanized forest harvesting in Czechia. Scand J For Res 34(7): 617–626. https://doi:10.1080/02827581.2019.1650952

Kozak, A., Yang, R.C., 1981: Equations for estimating bark volume and thickness of commercial trees in British Columbia. For Chron 57(3): 112–115. https://doi:10.5558/tfc57112-3

Li, R., Weiskittel, A.R., 2011: Estimating and predicting bark thickness for seven conifer species in the Acadian Region of North America using a mixed effects modeling approach: comparison of model forms and subsampling strategies. Eur J For Res 130(2): 219–233. https://doi:10.1007/s10342-010-0423-y

Löwe, R., Sedmíková, M., Natov, P., Jankovský, M., Hejcmanová, P., Dvořák, J., 2019: Differences in Timber Volume Estimates Using Various Algorithms Available in the Control and Information Systems of Harvesters. Forests 10(5): 388. https://doi:10.3390/f10050388

Marshall, H.D., Murphy, G.E., Lachenbruch, B., 2006: Effects of bark thickness estimates on optimal log merchandising. For Prod J 56(11/12): 87–92.

Miles, P., Smith, W., 2009: Specific gravity and other properties of wood and bark for 156 species found in North America research Note NRS-38. Newtown Square, PA: U.S. Forest Service, 35 p. https://doi:10.2737/NRS-RN-38

Muhairwe, C.K., 2000: Bark thickness equations for five commercial tree species in regrowth forests of Northern New South Wales. Aust For 63(1): 34–43. https://doi: 10.1080/00049158.2000.10674811

Natov, P., Dvořák, J., Sedmíková, M., Löwe, R., Ferenčík, M., 2017: Srovnání vyrobeného objemu dříví harvestorem se zásobou porostu stanovenou objemovými tabulkami (Comparison of harvester-produced timber volume with the standing timber volume determined by volume tables). Zpravy Lesn Vyzk - Reports For Res 62(1): 1–6.

Pásztory, Z., Mohácsiné, I., Gorbacheva, G., Börcsök, Z., 2016: The Utilization of Tree Bark. BioResources 11(3): 7859–7888.

Pausas, J.G., 2015: Bark thickness and fire regime. Funct Ecol 29(3): 315–327. https://doi: 10.1111/1365-2435.12372

PHP.net, 2019: Function array-rand.php, PHP manual. Available online: https://www.php.net/manual/en/function.array-rand.php (Accessed 10 October 2020)

Purwestri, R.C., Hájek, M., Šodková, M., Sane, M., Kašpar, J., 2020: Bioeconomy in the National Forest Strategy: A Comparison Study in Germany and the Czech Republic. Forests 11(6): 608. https://doi:10.3390/f11060608

Purwestri, R.C., Hájek, M., Šodková, M., Jarský, V., 2020: How Are Wood and Non-Wood Forest Products Utilized in the Czech Republic? A Preliminary Assessment of a Nationwide Survey on the Bioeconomy. Sustainability 12(2): 566. https://doi:10.3390/su12020566

Sáenz-Esqueda, M.A., Rosales-Castro, M., Rocha-Guzmán, N.E., Gallegos-Infante, J.A., González-Laredo, R.F., 2010: Phenolic content and antioxidant action in needle extracts from Pinus cooperi, P. durangensis, P. engelmanii and P. teocote. Madera y Bosques 16(3): 37–48.

Sedmíková, M., Löwe, R., Jankovský, M., Natov, P., Linda, R., Dvořák, J., 2020: Estimation of Over- and Under-Bark Volume of Scots Pine Timber Produced by Harvesters. Forests 11(6): 626. https://doi:10.3390/f11060626

Skogforsk, 2012a: Project StanForD Bandic Documents. (last update 2012-04-18). The Forest Research Institute of Sweden. Upssala: Sweden. Available online: https://www.skogforsk.se/english/projects/stanford/ (Accessed 1 November 2020)

Skogforsk, 2012b: Standard for Forest Data and Communications. Appendix: Definitions of variables – General and country specific. (last update 2012-04-18). The Forest Research Institute of Sweden. Upssala: Sweden. Available online: https://www.skogforsk.se/cd_20190114161714/contentassets/b063db555a664ff8b515ce121f4a42d1/appendix1_eng_120418.pdf (Accessed 1 November 2020)

Stängle, S.M., Sauter, U.H., Dormann, C.F., 2017: Comparison of models for estimating bark thickness of Picea abies in southwest Germany: the role of tree, stand, and environmental factors. Ann For Sci 74(1): 10. https://doi:10.1007/s13595-016-0601-2

Strandgard, M., Walsh, D., 2011: Improving harvester estimates of bark thickness for radiata pine (Pinus radiata D.Don). South For 73(2): 101–108. https://doi:10.2989/20702620.2011.610876

Vaucher, H., 2003: Tree bark: A color guide. Timber Press, Portland–Cambridge, 260 p.

Wehenkel, C., Cruz-Cobos, F., Carrillo, A., Lujan-Soto, J.E., 2012: Estimating bark volumes for 16 native tree species on the Sierra Madre Occidental, Mexico. Scand J For Res 27(6): 578–585. https://doi: 10.1080/02827581.2012.661453

West, P.W., 2015: Tree and forest measurement, 3rd edn. Springer, Cham, 214 p.

Wojnar, T., 2007: Doporučená pravidla pro měření a třídění dříví v České republice 2008 (Guidelines for timber scaling in the Czech Republic 2008). 2nd ed. Kostelec nad Černými lesy, Czech Republic: Lesnická práce, 147 p.

Zacco, P., 1974: Barktjockleken hos sågtimmer. Rapport nr. 90. Inst. för Virkeslära, Skogshögskolan, 1–53.

Zeibig-Kichas, N.E., Ardis, C.W., Berrill, J.P., King, J.P., 2016: Bark thickness equations for mixed-conifer forest type in Klamath and Sierra Nevada mountains of California. Int J For Res 2016: article ID 1864039. https://doi:10.1155/2016/1864039

© 2022 by the authors. Submitted for possible open access publication under the
terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Authors' addresses:

Assist. prof. Martin Jankovský, PhD

e-mail: jankovskym@fld.czu.cz

Assist. prof. Jiří Dvořák, PhD

e-mail: dvorakj@fld.czu.cz

Radim Löwe, PhD *

e-mail: lowe@fld.czu.cz

Pavel Natov, PhD

e-mail: natov@fld.czu.cz

Ondřej Nuhlíček, Ing.

e-mail: nuhlicek@fld.czu.cz

Czech University of Life Sciences Prague

Faculty of Forestry and Wood Sciences

Kamýcká 129

165 00 Praha – Suchdol

CZECH REPUBLIC

* Corresponding author

Received: April 2, 2021

Accepted: April 28, 2022

Original scientific paper